“摩擦”选项卡

本页面阐述使用原生 Simulation Mechanical（SimMech) 求解器运行的非线性模拟中通用面对面接触的摩擦参数。这些参数位于“接触选项”对话框的“摩擦”选项卡中。仅当您激活“常规”选项卡下的“包含摩擦”选项时，才会显示此选项卡。

在无摩擦的接触中，单元刚度矩阵是对称矩阵。如果存在摩擦，矩阵将变成不对称矩阵。使用不对称求解器的计算成本高于使用对称求解器的成本。为了提高效率，MES 强制单元刚度对称，以便使用对称求解器求解摩擦接触。

如果在分析中考虑摩擦接触，则求解过程极易受到滑动过程的干扰和影响。接触表面开始滑动后，滑动之前的平衡状态将不再有效，处理器必须在求解过程中尝试找到新的平衡状态。此外，对称近似可能会导致收敛效果不佳。每个可用的摩擦定律选项都会尝试以不同的方式控制求解不稳定性。

从位于“摩擦力”选项卡顶部的下拉菜单中选择所需的“摩擦定律:”。有三种选项可用于 Simulation Mechanical 中的非线性面对面接触：

在随后的子部分中将讨论每个摩擦定律及其适用的参数。

修正的库仑摩擦

此摩擦定律使用经典摩擦算法：库仑摩擦。在基础库仑摩擦模型中，两个接触表面在发生相对滑动之前，可以承受一定大小的剪切应力（由摩擦系数和法向接触压力决定）。库仑摩擦模型如下定义：τ = μ，其中 μ 是摩擦系数，P 是法向接触压力。当使用“修正的库仑摩擦”定律时，您必须定义下列三个参数：

理想情况下，剪切应力超过 μsP（通过“静摩擦系数”输入得出）后，两个表面将开始滑动。此外，剪切应力将变为 μdP，此时使用的是“滑动摩擦系数”值。

从数字上很难实现理想情况（剪切应力超过静态值之前无运动），如图 1 所述。因此，在使用此摩擦定律时需要定义“切向刚度比”。“切向刚度比”是切向接触刚度 (Kt) 与法线方向接触刚度 （K) 之间的比值，这在“高级”选项卡下进行定义。（请参见本页的“‘高级’选项卡”部分。）切向刚度越大，精度越高，但所需迭代也越多。切向刚度越小，提供的收敛效果越好（运行时间越短），但可能会降低精确度。建议的值范围是 0.01 到 1。鉴于静摩擦系数会变大，建议使用较小的切向刚度比。

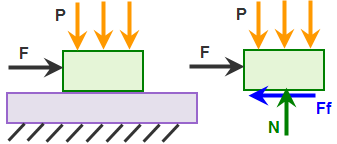
提示： 为了防止振动延长分析运行时间，不应使用大小相似的静摩擦系数和滑动摩擦系数。

(a) 模型和顶部块体的自由体受力图。作用力 F 随时间不断增大，直到超过静摩擦力。

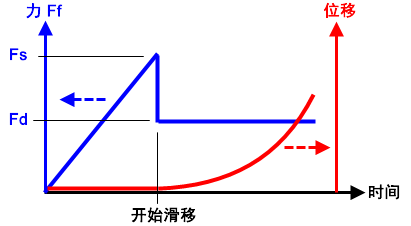
(b) 摩擦力 Ff 与时间的关系图（蓝色曲线）和位移与时间的关系图（红色曲线）。摩擦力 Ff 达到静摩擦力限值 (Fs = μs * N) 前，部件不运动。超过静摩擦力后，摩擦力 Ff 将从 Fs 下降到 Fd (= μd * N)，部件开始加速。

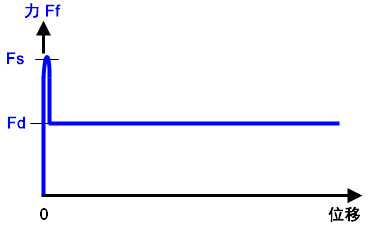
(c) 组合 (b) 中的图形以显示摩擦力与位移的关系。理想情况下，在摩擦力达到 Fs 后才会发生位移，之后便开始滑动。从数字上来说，这种情况很难实现，因为只要存在位移即暗示摩擦力为 Fd。

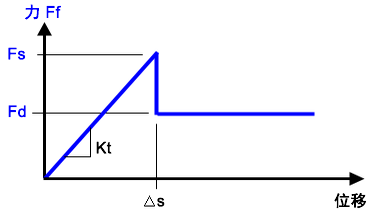
(d) 为了避免 (c) 中的数值不稳定性，当摩擦力小于静态限值 (Fs) 时，允许部件出现小幅度位移 (Δs)。运动量通过切向刚度 (Kt = Fs/Δs) 控制。较小的 Kt 值允许部件在开始滑动前移动较大的位移且更易于收敛；而较大的 Kt 值（较陡的斜坡）允许部件在开始滑动前移动较小的位移且难以收敛。切向刚度的计算公式为切向刚度比 x 法线方向的刚度。

图 1：修正的库仑摩擦的切向刚度

库仑与粘性摩擦

与修正的库仑摩擦定律不同，库仑与粘性摩擦定律不会同时考虑静摩擦系数和动摩擦系数。在“修正的库仑摩擦”定律中，需要相对较大的力来克服静摩擦并开始运动。滑动开始后，摩擦力将降低，因为滑动摩擦系数小于静摩擦系数。因此，摩擦力突变将造成力的不连续性。在“库仑与粘性摩擦”定律中，滑动开始后不会出现摩擦力不连续。相反，随着滑动速度不断增加，摩擦力将逐渐变大。

必须为“库仑与粘性摩擦”选项定义两个参数：

图 2：摩擦力与滑动速度的关系（库仑与粘性摩擦）

在图 2 中，摩擦力 (Ff) 曲线定义如下：

Ff = Fd + νf Vt
其中
Fd 为动（滑动）摩擦力，
νf 为粘性摩擦系数，
Vt 是两个部件之间的切向（滑动）速度。

如果 νf = 0，则 Ff = Fd

Smooth Coulomb friction

与“库仑与粘性摩擦”定律一样，“Smooth Coulomb friction”定律仅考虑滑动摩擦系数。这消除了使用“修正的库仑摩擦”定律时静态和滑动条件之间出现的摩擦力不连续性。静态和滑动条件之间的过渡将因包含平滑过渡因子 (Φ) 得到进一步稳定。

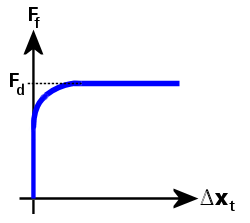
图 3：摩擦力与切向相对位移的关系（平滑库仑摩擦）

在图 3 中，摩擦力 (Ff) 曲线定义如下：

Ff = Fd Φ，
Φ = tanh(3 Δxt / δ)
其中
Fd 为动（滑动）摩擦力。
Φ 是过渡因子，它可使得摩擦力随着切向相对位移逐渐接近零而平滑地接近零。同样，它可使得摩擦力随着切向相对位移逐渐增加而平滑地接近动摩擦力。
Δxt 是切向相对位移，
δ 是基于接触刚度和动摩擦力计算的容差。
父主题： Simulation Mechanical 表面接触选项（非线性）