Mooney-Rivlin 材料模型是超弹性材料模型,可用于二维、块体、四面体、膜和壳单元。下文将列出 Mooney-Rivlin 材料属性。除了这些属性以外,可能还需要定义一些各向同性材料属性。
单击“单元材料定义”对话框上的“曲线拟合”按钮可使用曲线拟合程序。此程序可使用测得的应力-应变数据计算材料常数。
不同阶次的材料的位势函数如下所示:
2 阶常数标准:
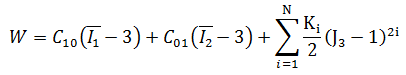
5 阶常数高阶:
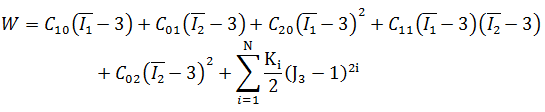
9 阶常数高阶:
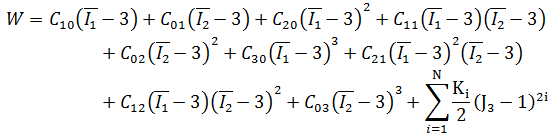
无论为何种阶次,初始剪切模量 μ0 和体积模量 k0 仅取决于阶次 N = 1 的多项式系数:
μ0 = 2(C10 + C01),k0 = K1
Mooney-Rivlin 形式可以视为 neo-Hookean 形式的扩展,因为它添加了一个取决于左侧 Cauchy-Green 张量的第二个不变量的项。在某些情况下,与 neo-Hookean 形式相比,此形式可为实验数据提供更精确的拟合。但是,通常这两个模型会提供类似的精确度,因为它们仅使用不变量的线性函数。这些函数无法表示应力应变曲线中较高应变级别处的“回升”。
弹性体积模量:
弹性体积模量可以通过以下表达式得到:E/3 * (1-2v),其中 E 是材料的弹性模量,v 是材料的泊松比。
第一个和第二个常数:
可以变化 Mooney-Rivlin 表达式 σ = 2(C1 + C2/λ)(λ - 1/λ2) 以得到以下形式:σ / [2(λ - 1/λ2)] = C2 + λ-1 + C1。这类似于 y=mx+b 形式的线性表达式,其中...
- m 是斜率,对应于第二个 Mooney-Rivlin 常数 C2
- b 是 y 截距,对应于第一个 Mooney-Rivlin 常数 C1
(较高阶次的材料模型和上面的位势方程分别将第一个和第二个常数称为 C10 和 C01。)
注: Mooney-Rivlin 表达式已通过不同的源写成不同的形式。在软件中使用 Mooney-Rivlin 常数时,请确保为 C1 和 C2 输入的值与 σ 的关系完全如上文所述的方程所示。此外,请确保整个数据输入和建模过程中单位保持一致。