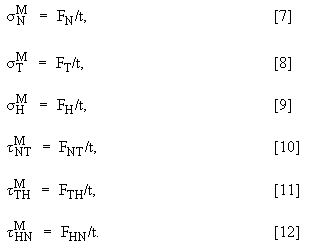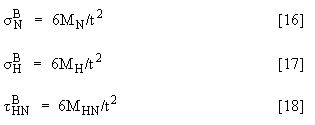此页面将介绍如何计算主膜应力和主弯曲应力（Pm 和 Pb）。
这些应力的计算包括多个步骤。首先重新计算应力分类线 (SCL) 指定的局部坐标系中的六个全局应力张量。然后，使用以下公式沿 SCL 对六个局部应力张量（σN、σT、σH、τNT、τTH、τHN）求积分，以获得总载荷（FN、FT、FH、FNT、FTH、FHN）：
其中 T 是沿 SCL 的位置。
然后，为所有 6 个分量计算膜应力 (F/A)。对于长度为 t 的 SCL，
主膜应力 (
) 将通过分量由方程 7 到 12 给出的张量获得。这些应力通过重算主轴方向的此张量获得。
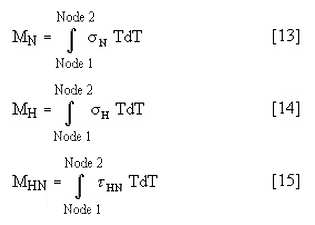
接下来，将通过从总应力分布减去膜应力求出弯曲应力。该过程是逐个应力点进行的。首先，为长度为 t 的 SCL 求出力矩载荷分布。然后，对力矩载荷分布求积分以获得横截面上的力矩。
应使用梯形积分计算这些积分。后续结果用于通过以下公式计算长度为 t 的 SCL 的弯曲应力 (Mc/I)：
下一步是计算 SCL 各端的主应力 (
)。这些主膜应力加上弯曲应力由分量通过替换 T = 节点 1 和 T = 节点 2 获得的张量计算得出。
膜应力通过方程 7 到 12 获得，弯曲应力通过方程 16 到 18 获得。注意有两组主应力：一组是当 T = 节点 1 时，另一组是当 T = 节点 2 时。同样，主应力通过重算主轴方向的张量获得。
此时已获得所有主膜应力、
以及主膜应力和弯曲应力之和，
需要这些值才能确定输出标量：
- Pm 和
- Pm + Pb
将根据两种不同的组合方法（最大剪切应力和 Von Mises 应力）计算和输出这两个标量值。下表列出了用于每个值和计算方法的方程：
| 表 1：每种计算方法的 Pm 和 (Pm + Pb) 方程 | |||
|---|---|---|---|
| 最大剪切应力方法 | Von Mises 应力方法 | ||
|
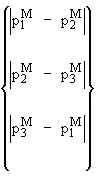
Pm = 以下项最大值：
|
[25] |
|
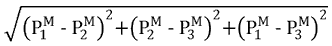
[27] |
|
(Pm + Pb) = 以下项的最大值：
|
[26] * |
|
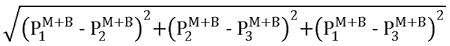
[28] * |
* 注意：方程式 26 和 28 必须都计算两次，因为存在两组值：一组是当 T = 节点 1 时，另一组是当 T = 节点 2 时。输出量以具有最大结果值的节点为基准。
最后，通过以下应力组合方法简单的差值方程式计算得出主弯曲应力强度 (Pb)：
Pb = (Pm + Pb) - Pm[29]
参考：ASME SGDA-99-2，针对小组委员会的拟议非必要附录 III & VIII，有限元分析应力结果的解释，第 4 版，2000。