钢筋混凝土的理论描述

尽管具有不同的拉伸性能和压缩性能，钢筋混凝土材料模型在统计学上仍被视为同类。它遵从涂抹式裂纹模型，通过积分点处弹性的衰减来模拟破裂和破碎过程，而不是通过跟踪各个宏观裂纹进行模拟。本文所述的模型用于相对单调的载荷。（真正单调的载荷可增可减，但不得反向。）在当前模型中，尽管破裂被认为最重要的方面，但还应合理考虑约束导致的压缩情况。

此外，钢筋混凝土的材料模型还采用弥散式钢筋方法。钢筋假定使用给定的体积分数分布（弥散）在整个单元中。钢筋的强度将加强指定方向上的混凝土。钢筋材料本身采用 von Mises 双线性等向强化的弹塑性材料模型。您可以定义三个独立的钢筋方向。

图 1 显示了普通混凝土的典型单轴行为。当混凝土以压缩形式加载时（点 3-2-1），它在达到屈服点（点 2）之前均呈弹性变化。该材料将对软化做出响应，并出现不可恢复的变形。达到峰值强度的破坏点（点 1）之后，材料将会受损，但理论上仍可承载部分载荷。目前，这种压缩软化效应不会通过分析加以建模，混凝土将视为受挤压，且随后无法再承载任何载荷。破坏之前的卸载被视为弹性行为，且遵循杨氏模量。

当混凝土以拉伸形式加载时，它在达到破坏强度（点 4）之前均呈弹性变化。对钢筋混凝土中各裂纹的载荷传递（拉伸硬化）进行建模时，受拉伸作用的破坏后行为（拉伸软化）非常重要。

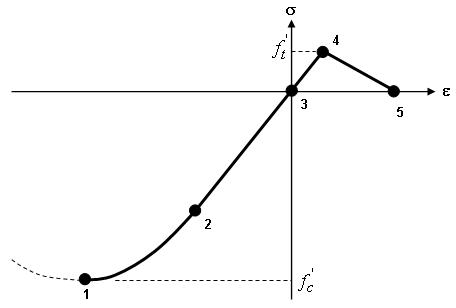
 图 1：普通混凝土的理想化单轴行为

破坏准则

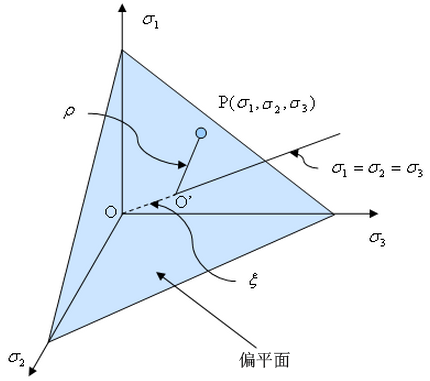
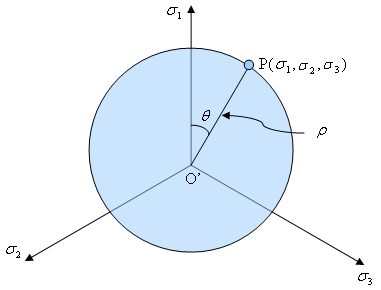
在主应力空间中操作时十分便捷，该空间中的任何应力状态均由 Haigh-Westergaard 坐标 (x, r, q) 定义：

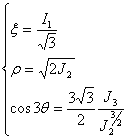(1)

其中，I₁ = δ_ijσ_ij，J2 = 0.5S_ijS_ij，J3 = (S_ijS_jkS_ki)/3，且 S_ij = σ_ij - (δ_ijσ_kk)/3。

(a) 主应力空间

(b) 主应力投影的应力平面

图 2：Haigh-Westergaard 应力坐标

该分析使用与 Hsieh-Ting-Chen (HTC) 四参数准则（参考文献 1）类似的破坏准则，但通过 William-Warnke 五参数准则（参考文献 2）的应力半径表示法引入依赖效应。

(2)

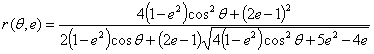(3)

其中，f_t' 和 f_c' 分别是单轴拉伸和压缩强度（绝对值），e 是 Kang 和 Willam 定义的离心率：

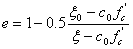(4)

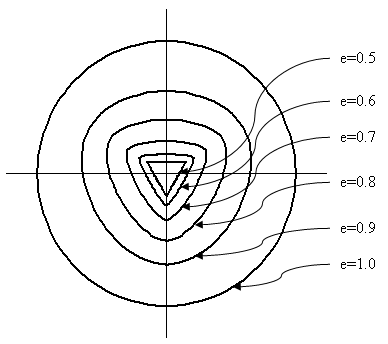
其中，c ₀ 是可通过实验校准的材料常数（在 Kang-Willam 准则（参考文献 5）中设置为 5.5）。等三轴拉伸强度 ζ ₀ =sqrt(3)f _t '。离心率 1 是应力平面中的圆（图 3），且破坏与 Lode 角 ϑ 无关。

屈服面的载荷假定为通过单个参数 k 从初始屈服面膨胀至最终破坏面的载荷。该参数的值介于 k ₀ （在初始屈服点处）到 1（在破坏点处）之间。根据 Imran-Pantazopoulou 准则（参考文献 4），中间破坏面与静水轴的交点由另一术语确定。

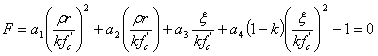(5)

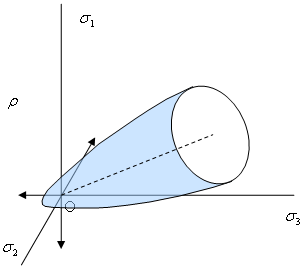
此外，该分析还通过引入拉伸截止（最大拉伸应力或兰氏温标准则），假定拉伸显著状态不存在屈服。在拉伸-压缩混合区域（参考文献 1）中，屈服面将逐渐发生变化。因此，破坏包络面是主应力空间中的开曲面，如图 3 中所示。如果存在主拉伸应力，则该分析始终假定破坏为破裂。由于混凝土无法使用复杂方法，从而导致某些研究无法区分破坏类型，因此这种假定未免有些武断。

(a) 混凝土的破坏包络面

(b) 混凝土破坏包络面的应力视图

图 3：破坏包络面

压缩硬化

为了简便起见，当混凝土主要承受压缩载荷时，我们使用关联的流动和双线性等向应变硬化。此方法可得出对称控制方程，且计算效率较高。但是，它通常会高估塑性体积应变。

在拉伸-压缩混合域（参考文献 1）中，屈服面将修改为在边界处与原点相切的表面（图 4）。

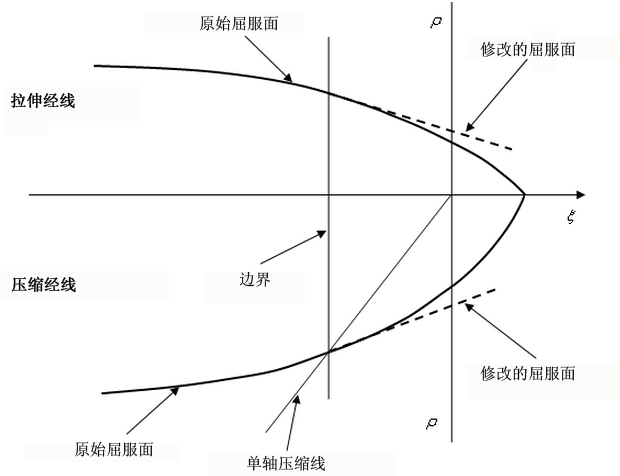
图 4：拉伸-压缩混合域中的屈服面

应力更新是通过全隐式 Backward Euler 返回映射方案完成的，该方案要求进行大量计算。

拉伸硬化

当至少一个主应力在破坏面拉伸时，我们便假定已出现破裂。该分析使用破坏弹性对破裂的混凝土进行建模。假定没有永久应变与裂纹相关。

为了克服与拉伸软化相关的网格敏感性，该分析假定断裂能（每单位面积）G_f 是材料属性。特定的断裂能（每单位体积）g_f 与 G_f 相关，计算公式如下：

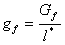(6)

其中，l* 是积分点处的特征长度或裂纹带宽（参考文献 6）。

剪力保持系数 b 由用户指定。值 1 表示极致粗糙的裂纹，其中剪切力将完整传递。值 0 表示极致平滑的裂纹，其中剪切力无法传递。与破裂相关的泊松比效应（侧向膨胀）将会忽略。裂纹闭合后，压缩应力可完整传递。

破坏面的定义中不包括与开口裂纹关联的应力分量，这样可进一步检测同一积分点处的破裂情况。

计算破坏包络面

如上所述（方程 2，其中 ρ = 0），₃ 由等三轴状态确定。其他破坏面参数（a₁、a₂ 和 c₀）通过三种独立应力状态下的非线性方程（方程 2、3、4）求解得出。对于其他实验组合，用户必须先计算这些参数，然后再直接输入。

对于硬化参数（a₄ 和 k₀）,该分析假定非均匀加工硬化由其他硬化术语（方程 5）确定。为简便起见，假定硬化对有效塑性应变 () 和静水压力 (ζ) 的依赖性可分离。有效塑性应变 () 仅影响硬化参数 k。因此，用户可以根据单轴压缩实验校准 a₄ 和 k()。

注： 非线性校准方程可能存在多个解。此外，由于实验数据分散，因此如果仅使用最少实验次数，则拟合度可能较低。

参考文献

1. Chen, W.F. 和 Han, D.J., Plasticity for structural engineers, Springer, 1998
2. Willam, K. 和 Warnke, E., Constitutive model for triaxial behavior of concrete.International Association for Bridge and Structural Engineering, Zurich, pp.1-30, 1975
3. Kupfer, H. 和 Gerstle, K., Behavior of concrete under biaxial stresses, Journal of Engineering Mechanics, v99, n4, pp 853-866, 1973
4. Imran I. 和 Pantazopoulou S., Plasticity model for concrete under triaxial compression.Journal of Engineering Mechanics, v127, n3, pp.281-290, 2001
5. Kang, H. 和 Willam, K., Localization characteristics of triaxial concrete model, Journal of Engineering Mechanics, v125, n8, pp941-950, 1999
6. Crisfield, M.A., Non-linear finite element analysis of solids and structures, Vol.2: Advanced topics, J. Wiley & Sons, New York, 1997