摘要
实体模型的有限元分析 (FEA) 精度通常受益于由高几何质量单元组成的网格。Autodesk Simulation 开发了一种自动化实体网格划分方法,可强制执行 NASTRAN 处理器使用的严格几何模型检查。自动生成实体单元可能导致网格的内部空隙较小。通常,仅当考虑形状复杂的部件(包括 CAD 实体网格)时才会出现此类空隙。本章讨论使用包含此类空隙的网格获取的结果。自动网格划分方法已经过优化,能够最小化这些空隙的尺寸,这就是所谓的“微孔”。这些结果可与使用全填充式部件获取的其他结果和分析解进行比较。我们将展示含微孔的模型和含全填充式网格的模型如何生成无明显差异的结果。
简介
若要将 FEA 应用于三维实体模型,则需要生成仅由四面体单元组成或由块体、楔形体、锥体和四面体混合组合的网格。如果考虑使用四边形表示表面的实体,则后者更佳。您还可进一步优化该方法,避免生成锥体。适当尝试生成网格,构建符合 NASTRAN 等规范的最优单元。通常,自动网格生成器旨在以较低的纵横比生成单元。Autodesk Simulation 的自动实体网格生成器不仅可最小化纵横比,而且还能构建符合 NASTRAN 处理器所采用的几何模型检查的单元。这些几何检查包括:纵横比,坍塌率、锥度比、内角、倾斜角、扭曲角和扭曲系数。
最好使用仅由符合高质量标准的单元(如上述单元)组成的网格完全填充实体。此类网格应当能够生成非常精确的 FEA 结果。但问题是,对于包含复杂几何体的模型,并非总能获取此类网格。这主要是因为详细的几何特征将约束网格生成器,防止在小型单元尺寸和大型单元尺寸之间创建渐变的网格。CAD 模型的出现使具备详细特征的模型普遍化。如果使用等于或小于特征尺寸的网格尺寸,则无需过渡,并且可对所有全填充式部件强制执行高质量约束。然而,此方法要求网格尺寸非常小,并使用数量不切实际的单元生成模型,从而导致求解需要过度的计算资源。毕竟,工程师的目标通常是在确保方法实用的同时,最大限度地提高精度。
为了避免生成要求不切实际的极精细网格,以满足填充实体和高单元质量约束,我们开发了一种自动网格划分方法,将尺寸可以忽略不计的空隙保留在实体内。此方案旨在通过构建仅符合严格几何质量标准的单元,实现可能的最高精度。我们还开发了另外一种自动网格划分方法,该方法首先应用高质量网格划分方法生成微孔,然后使用不一定要符合几何模型检查的单元填充小空隙,以此完全填充部件。如下所述,具有微孔的网格和少数单元违反几何模型检查的完整网格均不会导致精度明显降低。毕竟,与自动生成的常用 FEA 网格相比,后一种网格无疑具有明显改进。此类网格可能有很多劣质的单元,占据了整个体积的很大一部分。
上述这两种网格划分方法通过使用推进算法从表面向内构建单元来解决这个问题。此方法通常会在表面附近生成符合严格几何模型检查的单元,仅在部件深层生成微孔或低质量单元。为精准起见,宜将最优单元放在表面附近,此处 FEA 求解的梯度通常最大。这是因为在大多数 FEA 应用(包括应力分析)中,载荷和约束以及部件间作用通常发生在表面上。
在本章中,我们将介绍微孔如何生成相比包含全填充式网格的对比模型明显更精确的 FEA 结果。根据拉格朗日公式获得了分析类型的结果,包括应力、热和静电。具有微孔的模型不适用于欧拉公式,例如,流体流动分析。
比较研究
通过将具有和没有微孔的模型结果进行比较,检查微孔对 FEA 求解产生的影响。具体地说,我们将通过使用两种不同的网格划分方法获取实体网格的相同表面网格进行比较。为了集中精力研究微孔效应(而非网格类型),我们仅考虑使用 Autodesk Simulation 混合实体网格类型的网格。在四面体或混合实体网格类型中,如果无法构建四面体单元来填充给定的小空隙,则会出现微孔。对于这两种网格划分方法,仅在最终的网格划分阶段中生成四面体单元。这项研究中考虑的模型最初可能具有相对简单的几何体,缺乏被视为微孔根源的小特征。然而,由于使用局部网格细化,导致表面网格尺寸陡然转变,促使生成微孔。需要指出,本章中介绍的所有模型均包含典型到较大体积分数的微孔,从而能够最大限度地发挥其作用。
图 1 描述了三部件 CAD 装配件的表面几何。此表面网格生成了相对较大的微孔体积分数 0.00207。针对此模型及其全填充式部件执行了“线性材料模型静态应力”和“固有频率(模态)”分析。图 2 显示了如何针对这两个模型版本获取类似的应力结果。利用模态分析获取前五个固有频率,而正如表 1 所示,这两个模型版本再次得出并无明显工程差异的解。

图 1:粘合到两个支架的圆形杆的三部件装配件 FEA 模型(包括网格),这些支架通过对位于平端(底面上的红色三角形)的孔边使用边界条件予以修复。在“线性材料模型静态应力”分析中,对圆形杆的一端(黄色箭头)施加 5.0 x 108 达因的表面力。
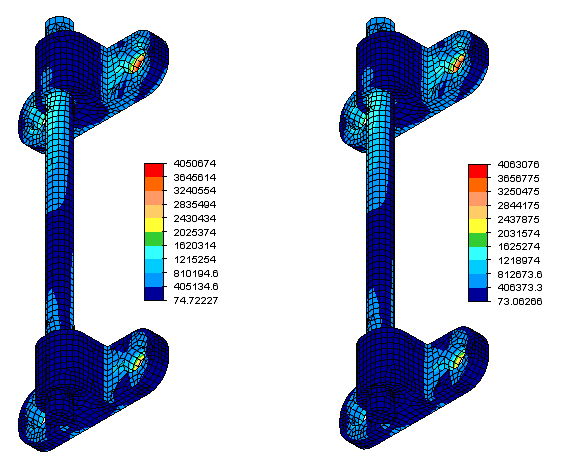
图 2:从粘合到两个支架的圆形杆的三部件装配件的“线性材料模型静态应力”分析获取的 von mises 应力分布。左侧图是没有微孔的模型,而右侧图则是具有微孔的模型。后者预测的最大应力比前者大 0.31%。
|
模数 (n) |
没有微孔的模型 |
具有微孔的模型 |
差异百分比 (%) |
|
1 |
1132.8 Hz |
1129.2 Hz |
0.318 |
|
2 |
1169.9 Hz |
1168.1 Hz |
0.154 |
|
3 |
1228.1 Hz |
1226.1 Hz |
0.163 |
|
4 |
2877.4 Hz |
2875.0 Hz |
0.083 |
|
5 |
3007.0 Hz |
3003.2 Hz |
0.126 |
|
表 1:从粘合到两个支架的圆形杆的三部件装配件的“固有频率(模态)”分析中获取的模态频率。请注意,所有这些频率之间的差异均在 0.32% 内。 |
|||
图 3 描述了具有和没有微孔的单部件圆环模型的“稳态热传递”结果。微孔导致更典型的体积分数 0.00046。正如在“线性材料模型静态应力”分析中一样,两个模型版本生成的结果也非常类似。图 4 显示了使用 Autodesk Simulation 的机械运动仿真 (MES) 软件为两个圆环模型版本获取的位移结果。即使对于非线性 FEA,微孔的存在也未明显影响结果。最后,图 5 显示了使用 Autodesk Simulation 的“静电流和电压”分析为两个模型版本获取的电压结果。正如预期的那样,由于静电分析与热分析之间有着潜在的相似之处,因此微孔的存在对结果影响不大。

图 3:从圆环模型的“稳态热传递”分析获取的温度分布,其中,底座温度保持在 100°F,施加给内表面的热通量为 0.642 BTU/(sec . in2)。左侧图是没有微孔的模型,而右侧图则是具有微孔的模型。后者预测的最高温度比前者高 0.349°F。

图 4:从环状模型的“机械运动仿真 (MES)”分析获取的位移大小分布,其中,外表面固定,施加给内表面的时间比例式压力达到最大值 100 lb/in2 秒。0.1 秒事件结束时将显示结果。左侧图是没有微孔的模型,而右侧图则是具有微孔的模型。后者预测的最大节点位移比前者大 0.56%。

图 5:从环状模型的“静电流和电压”分析获取的电压分布,其中,对顶面的内边施加 100 V 电压,对外表面的外边施加 0 V 电压。左侧图是没有微孔的模型,而右侧图则是具有微孔的模型。通过比较外部顶边上的最大点电,结果表明两个模型之间的差异为 0.02%。
结论
现已开发一种着重于精度的新型自动网格划分方法。此方法仅生成高几何质量的单元,但保留微孔。此网格划分方法经过扩展,能够使用可能不满足高几何质量约束的单元填充这些小空隙。这两种方法生成的网格均能够产生高度精确的 FEA 结果。几个示例演示了具备典型到较大体积分数的微孔以及全填充式网格的 FEA 模型如何生成可与工程精度媲美的结果。