无论采用何种形式，有限元分析 (FEA) 最终旨在对方程组进行求解。以下面所示的两个简单弹簧模型为例，其中，F1 和 F2 是外施载荷，K1 和 K2 是弹簧刚度，X1 和 X2 是每端的变形。请记住，其中任一外施载荷可以为零，但都是已知值。每个弹簧由于延伸而产生的力未知，但可以通过直接公式 F = k*x 计算得出。鉴于弹簧 1 和 2 分别延伸 X1 和 (X2-X1)，我们可以写出对每个节点处的力进行求和的方程：
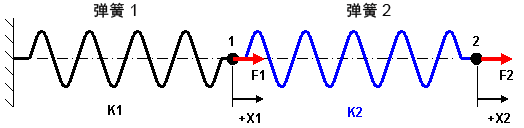
| F1 - K1*X1 + K2*(X2-X1) = 0 | 节点 1 |
| F2 - K2*(X2-X1) = 0 | 节点 2 |
重新排列方程后得出：
| F1 = (K1 + K2)*X1 - K2*X2 | 节点 1 |
| F2 = -K2*X1 + K2*X2 | 节点 2 |
这些方程可以矩阵形式表示，如下所示：
或者，用简化符号表示为 {F} = [K]{X}。
求解器将在 FEA 中求解方程矩阵。随着计算机硬件和计算技术的不断发展，此软件新增了许多新求解器。每一种分析均可选择各种求解器。在许多情况下，默认选项为“自动”。在这种情况下，此软件通常会根据模型尺寸（方程数）选择最适合分析的求解器。下文阐述了每种求解器的常规方法：
根据单元连接在一起的方式，刚度矩阵 [K] 通常非常稀疏。许多项为零。由于值零不会影响求解，因此大多数求解技术均以各种方式编程，以忽略零项。其中一种方法可以使用少量内存来存储矩阵，但需要优化才能最大程度地减少占用的内存；而另一种方法则使用更多变量来存储矩阵（因此需要更多内存），但整体速度更快。
接下来，方程组的求解方法将确定分析所需的时间。有些直接求解方法可以保证得出解，但前提是模型的设置正确无误（静态应力模型已经过正确约束，稳态热传递模型具有热源且能够散热等）。例如，高斯消元法和矩阵求逆等技术是便是简单的直接求解方法。此外，还有间接求解方法（已假设解）。通过将假设的解代入方程组，能够更好地估计每个未知数。重复此过程，直到解不再变化为止；因此，这些技术称为“迭代求解”。
最后，刚度矩阵在 FEA 中通常是对称的。在这些情况下，仅需存储不低于对角线的项。这样可以减少矩阵求解所需的内存数量和运算次数。如果考虑的效应导致矩阵变为非对称（例如，热传递分析中的体对体辐射或机械运动仿真中的激励器单元），则需要存储并运算整个矩阵。在这种情况下，求解时间将更长。
以下是常规求解器，它们在
使用原生 Simulation Mechanical 处理器时可用。
1
。对于特定的分析类型，每个求解器均有可能存在变化形式。例如，模态分析具有迭代求解器（子空间），这是在线性静态应力中可用的迭代求解器的变化形式（代数多重网格法，简称为 AMG）。从“设置”
“模型设置”“参数”中，设置用于分析的求解器类型（或者在树视图中的“分析类型”条目上单击鼠标右键，然后选择“编辑分析参数”）。
1 注意：Autodesk Nastran 编辑器和 Nastran 求解器存在类似下列选项的选项。但默认情况下，导出到 Nastran 编辑器或在 Simulation Mechanical 中运行（使用 Nastran 处理器）的所有分析均包括 DECOMPMETHOD=AUTO Nastran 求解器选项。有关修改特定于 Nastran 的求解器选项的信息，请参见 Autodesk Nastran 求解器选项页面。
稀疏求解器
- 为矩阵提供直接求解。
- 带宽未进行优化，因此节省了执行此运算所花的时间。
- 仅存储非零项，而非整个矩阵。（正因为如此，才出现了“稀疏求解器”这一术语。）
- 尽管要存储的刚度矩阵项更少，但需要更多变量才能存储非零项的位置。因此，稀疏求解器比其他求解器需要更多内存。
- 对于中小型模型，稀疏求解器的求解速度通常最快。
迭代求解器
- 为矩阵提供间接求解。因此，用户必须指定要执行的最大迭代次数，必须指定决定何时收敛解的收敛准则。不能保证在指定的迭代次数内求出矩阵解。
- 由于迭代求解器需要从初始猜测开始，因此某些处理器具有预调节器。这为提高模型求解效率提供了更多选项。
- 带宽未进行优化，因此节省了执行此运算所花的时间。
- 迭代求解器所需的内存比稀疏求解器更少。
- 对于大型模型，如果能够收敛，则迭代求解器的求解速度最快。大小取决于分析类型。对于线性静态应力而言，150,000 个方程（或自由度）属于大型模型。而对于需要求解大量时间步的机械运动仿真而言，50,000 个方程才有可能视为大型模型。 注意： 解的精确度取决于收敛容差；容差越小，解越精确，但所需的迭代次数也有可能越多。与所有迭代求解一样，您应检查结果，确认达到所需的精确度。在某些情况下，使用不同的收敛容差执行两次分析，这是确认精确度的最佳方式。注： 求解矩阵的迭代过程是一个必要的收敛级别。这提供了方程组的解。如果分析也是非线性的，则需要对问题反复求解，才能收敛到物理解。例如，辐射导致求解的方程成为非线性方程。这样一来，若要求出非线性方程的解，则需进行多次迭代。（通常，这些方程是线性的，且只需一个解。）请勿将求解模型的迭代过程与求解方程组的迭代过程混淆。提示： 如果该分析无法使用迭代求解器收敛，且显示消息“矩阵可能是非正定矩阵”或“预处理方程组的条件 =”，则问题可能是由于静态不稳定模型而引起的。在静态应力分析中，请确保所有组件均静态稳定。如果模型包括接触，请参见执行间隙单元分析页面中的建议。