梁预载会沿梁单元的长度创建轴向载荷。这可用于模拟紧固件、导线绳索和模型或部件内部的其他载荷(而不是外部载荷,如节点力)。与在整个分析中保持不变的外部载荷不同,如果结构的其余部分无限硬化,则预紧力数值是单元中的数值。由于结构并非无限硬化,因此预载会导致结构变形并释放部分预载。请参见下面的实际注意事项。
应用预载载荷
在线性分析中,梁预载仅适用于静态应力。它们不适用于载荷刚化固有频率(模态)和临界屈曲载荷。
在非线性分析中,梁预载适用于 MES 和非线性材料模型静态应力。您也可以在非线性材料模型固有频率(模态)分析中应用梁预载。但是,由于此分析类型不考虑载荷刚化效应,因此不会对结果产生影响。梁预载不适用于 MES Riks 法分析。
- 针对为要成为“梁”单元的部件,定义“单元类型"。
- 使用“选择”
 “选择”
“选择” “直线”命令,选择一个或多个梁单元。
“直线”命令,选择一个或多个梁单元。 - 在显示区域中单击鼠标右键,选择“添加”下拉菜单,然后选择“梁预载”命令向每个梁单元添加预载载荷。
- 在“轴向力”字段中输入预载大小。正值表示单元最初处于拉伸状态,因此该分析将梁端拉在一起。负值表示单元最初处于压缩状态,因此该分析将梁端分开。
- 对于受预载作用的梁单元,线段上有一个符号 B。若要修改预载,请在树视图的“FEA对象组”分支中选择预载条目,或者在线选择模式下在显示区域中选择 B 符号(“选择”
 “选择”
“选择” “直线”)。
“直线”)。
- 除了关联菜单命令之外,您还可以在功能区“设置”选项卡的“梁载荷”面板内单击“梁预载”命令。
- 初始应变视为零。因此,除非考虑预应变,否则计算应变看似与计算应力不符。
- 对于线性分析,预载应用于分析中的所有载荷工况。它不受任何载荷乘子影响。
- 对于非线性分析中的塑性材料模型,将计算预应变,因此效果会显示在应变结果中。
实用的注意事项
如前所述,由于构件将压缩以应对载荷,因此分析中会释放某些应用于梁单元的预载。如果提供的预载要成为最终载荷(例如,因使用扭矩扳手扭转螺栓而在转螺中产生的预载),则必须增加应用的梁预载以补偿部件压缩。如果构件刚度和最终载荷已知,则可根据以下公式计算要应用于梁单元的初始预载:
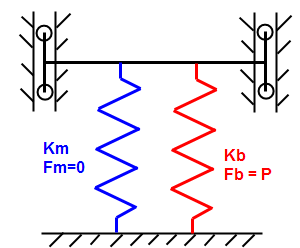
假设拉伸梁(用红色弹簧 K b 表示)以产生大小为 P 的预载,然后将梁附着到构件(用蓝色弹簧 K m 表示)。然后,梁和构件将压缩 Δ。由于梁在附着到构件并压缩构件之前会进行拉伸,因此梁中的最终载荷 F' 等于(预载-刚度)*压缩,而构件中的相等(但方向相反)载荷等于刚度*压缩。因此,有两个方程和未知数(F' 和 Δ)。
梁中的最终载荷 F' = P - KbΔ
构件中的最终载荷 F' = KmΔ
求解这两个最终载荷 F' 方程,得出
F' = P[Km/(K m +Kb)]
其中,Kb 是梁的刚度,Km 是构件的刚度,P 是应用于梁的预载。
对于螺栓连接,有很多公式计算构件的刚度,具体取决于对螺栓下的压力分布假设。此类公式如下所示,该公式考虑压力分布的顶角(30 度)和垫圈直径(相当于螺栓直径的 1.5 倍):

其中,L 是螺栓构件的总厚度,d 是螺栓和孔的直径。(参考文献:Budynas, Richard G 和 Nisbett, J. Keith, Shigley's Mechanical Engineering Design, McGraw-Hill, Inc, Eighth Edition)
此主题的所需项为 P/F' 比。在许多情况下,已知预载是螺栓和构件中的最终载荷 (F'),因此可以使用上述公式计算要应用于梁单元的预载 P。下表列出了几个结果。例如,当 L/d 为 2 时,要应用于梁单元的预载是螺栓和构件中的最终预载的 1.35 倍。(很显然,每个设计各不相同,因此上面的 Km 方程和下表是该方法的唯一表示。)
|
长度/螺栓直径 L/d |
预载/最终载荷 P/F' |
|---|---|
| 0.50 | 1.60 |
| 1.00 | 1.48 |
| 2.00 | 1.35 |
| 3.00 | 1.28 |
| 4.00 | 1.23 |
| 6.00 | 1.17 |
| 10.0 | 1.12 |
注释:
- 如果构件由多种材料组成,则可按串联弹簧计算刚度。请记住,在这种情况下,等效刚度 Keqv 的计算公式为:
1/Keqv = 1/K1 + 1/K2 + 1/K3。
- 如果一种材料明显弱于其他材料(例如,软质垫片材料),则相对较软的材料将起支配作用,且 Keqv ≈ Kgasket。
- 在某些临界情形下,如果未对模型应用载荷(预载除外),可能有必要执行分析,以确定获得最终载荷 F' 所需的预载 P。
使用温度将预载应用于模型部件时,可以采用类似的方法。