而實際上,大多數結構都將只在負載強度的限制範圍內展現出線性或近似線性的回應。在負載較高的情況下,結構勁度可能發生明顯改變,進而導致非線性回應。
對於簡單但真實的非線性圖而言,請考慮在頂部 (底部為鎖模,底部為自由) 受到水平力 H 與下降垂直力 V 的長度 L 細長柱。忽略尖端的少量下移,此類負載系統的主要影響將是會使柱的頂端橫向偏斜一定量,假設為 u。如果我們現在考慮此位移構形中的結構與負載,很明顯柱基上的彎矩 M 現在為:
M = HL + Vu
M 不僅僅只是外部負載的函數,還取決於 u 的這個事實,直接告訴我們問題是非線性的。很顯然,對彎曲柱起作用的垂直負載的影響將進一步增加橫向位移,使得直接對問題求解變得不可能。但是,我們可以將套用的負載 H 與 V 區分為小增量並將負載逐漸累積到所需等級,來接近真正的解。
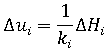
- i 是增量數目,
- ki 是柱尖端的目前橫向勁度。
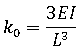
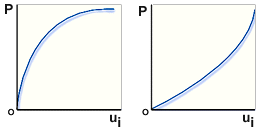
非線性回應的負載位移出圖
.左圖 軟化回應,右圖 硬化回應,P 非線性負載,ui 位移出圖
在上述範例中,我們使用了跟隨非線性負載撓曲路徑的逼近法 - 在此方法中,真正或確切的回應只能透過採取無限小的步長求得。若要瞭解非線性回應的更加確切模型的基礎,必須認清一點,即真實負載撓曲路徑上的每一點結構都必須處於平衡狀態。事實上,真正發生的事情是,隨著負載的增加,結構會採取連續構形,而每一個構形都是單獨由平衡確定的。因此,在負載位移空間中繪製的任何曲線能夠更正確地指稱為平衡路徑。在具有許多自由度的結構中,勁度矩陣的各係數將因負載量的不同而有不同的比率。因此,藉由針對套用的負載出圖不同位移元件所求出的平衡路徑看起來會不太一樣。看似任意選取要出圖的適當元件其實是強迫性的,因為完整 (一般性) 非線性回應會導致在 (N+1) 維負載位移空間中產生曲面 (在此 N 是結構的自由位移自由度數)。
平衡方程式
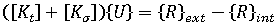
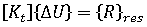
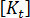 是目前構形的線性勁度矩陣。
是目前構形的線性勁度矩陣。 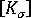 是目前構形的初始應力或幾何勁度矩陣。
是目前構形的初始應力或幾何勁度矩陣。 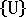 是增量節點位移的向量。
是增量節點位移的向量。 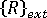 是等同於外部套用負載目前等級的節點力向量。
是等同於外部套用負載目前等級的節點力向量。 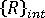 是等同於內部應力場的節點力向量。
是等同於內部應力場的節點力向量。 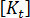 是目前構形的正切勁度矩陣。
是目前構形的正切勁度矩陣。 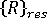 是目前構形中殘留 (不平衡) 節點力的向量。
是目前構形中殘留 (不平衡) 節點力的向量。
這些方程式為非線性,不可直接求解。但我們可以使用任何傳統預測-修正迭代技術 (例如牛頓-拉夫森或擬牛頓法),其左側做為預測器使用,右側做為修正器使用。在正常 (成功) 的迭代週期組中,結構的構形將向真正的平衡構形收斂,同時殘留非平衡力 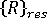 將變得任意小。實際上,當達到目標準確度 (由程式或您定義) 時,迭代便告終止。請注意,在平衡迭代期間,負載等級通常保持恆定。
將變得任意小。實際上,當達到目標準確度 (由程式或您定義) 時,迭代便告終止。請注意,在平衡迭代期間,負載等級通常保持恆定。
求解方法
- KSTRA=0:初始勁度方法
-
在這種成本很低但非常原始的方法中,初始線性彈性勁度
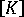 可用於所有負載增量及一個增量中的每一個迭代週期 (初始勁度方法)。由於位移增量的預測始終基於圍繞初始幾何的勁度矩陣的線性化,因此收斂可能非常慢,且在平衡路徑中遇到任何明顯的非線性情況時,演算法立即會失敗 (亦即發散或無法在指定迭代數之內收斂)。
可用於所有負載增量及一個增量中的每一個迭代週期 (初始勁度方法)。由於位移增量的預測始終基於圍繞初始幾何的勁度矩陣的線性化,因此收斂可能非常慢,且在平衡路徑中遇到任何明顯的非線性情況時,演算法立即會失敗 (亦即發散或無法在指定迭代數之內收斂)。 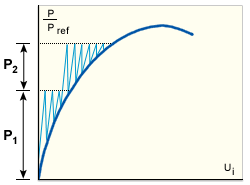
初始勁度方法
- KSTRA=1:修正的牛頓-拉夫森 (MNR)
-
此處會更新結構勁度矩陣並在每個負載增量開始時進行分解,亦即在上一步結束時得出平衡構形 (軟化結構的修正的 NR 方法和硬化結構的修正的 NR 方法)。然後會在不重新形成勁度的情況下執行迭代。此策略很適合中等非線性的平衡路徑零件。
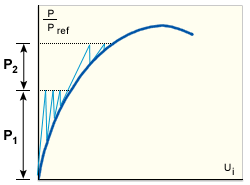
軟化結構的修正的 NR 方法
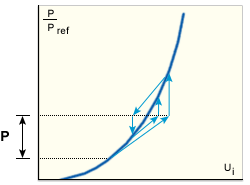
硬化結構的修正的 NR 方法
- KSTRA=2:NR 與 MNR 的組合
-
這是對於 MNR 方法的修正,在該方法中,勁度會在步長開始時及第一個迭代之後重新形成及進行分解 (硬化結構的結合的方法)。演算法可以處理中度非線性情形。
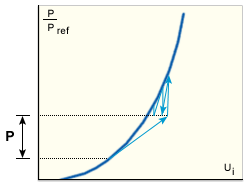
硬化結構的結合的方法
- KSTRA=3:牛頓-拉夫森 (NR)
-
在此情況下,結構勁度矩陣會在每個迭代週期開始時更新 (完整 NR 方法)。此方法會展示快速 (接近二次) 收斂,且適合處理平衡路徑中的嚴重非線性及分歧情形。但是,針對給定迭代數,它很明顯是目前為止最耗時的一項。
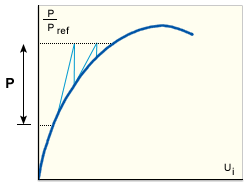
完整 NR 方法
- KSTRA=4:縮減步長的牛頓-拉夫森 (NR)
-
此策略與 KSTRA=3 相同,但使用此策略的目的是,當使用 KSTRA 3 遇到收斂困難時,將會使用步長大小的四分之一做為新步長,同時維持純 NR 迭代。
- KSTRA=5:負載步長
-
在此方法中,會暫時抑制平衡迭代。因此,針對每一個負載增量,只需要對結構勁度進行一次重新形成與縮減,且不會使用迭代 (直接前進到負載步長)。若要將真實平衡路徑的偏移降到最小,負載增量必須比在 MNR 或 NR 中使用的小很多,且必須使非平衡力前進 (與捨棄相反) 到下一的步長。此方法只做為當其他所有策略都失敗時才使用的最後解決方法。
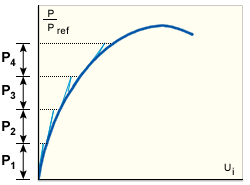
直接前進到負載步長
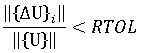
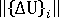 是兩個連續迭代之間節點位移變化的歐幾里得範數,亦即:
是兩個連續迭代之間節點位移變化的歐幾里得範數,亦即: 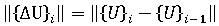
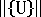 是目前總節點位移的歐幾里得範數。要使用的 RTOL 的適當值多少與問題有點相關,但您可預期位於 0.01 至 0.0001 範圍內的值提供足夠的準確度。
是目前總節點位移的歐幾里得範數。要使用的 RTOL 的適當值多少與問題有點相關,但您可預期位於 0.01 至 0.0001 範圍內的值提供足夠的準確度。 自動控制技術
非線性有限元素分析的其中一個主要困難是,沒有任何單一的迭代方法是所有求解路徑都適用的。當路徑的非線性情形變得更嚴重時,選取的策略可能會無法收斂,也無法進行後續動作。很明顯的,我們所需要的是能夠對無法使用不同步長大小與/或不同策略的步長使用新步長的自動控制系統。像這樣的方案可在分析中使用,並已證實在允許無需您介入的情況下自動追蹤求解路徑方面非常成功。方案的特性如下:
- 您選取初始最小策略 (通常為 KSTRA=1 或 2) 及初始步長大小。將會維持此策略,直到遇到收斂困難 (如果有) 為止。
- 在以下情況下視為發生收斂困難:
- 在允許的最大迭代數 Imax (預設值或您指定的值) 下未達到收斂,或
- 正在發散解 (如果針對 4 或更高的迭代,目前位移增量的範數
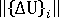 大於步長的第一個位移增量的範數
大於步長的第一個位移增量的範數 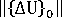 ,則會假設為發散解。非平衡力的歐幾里得範數大於套用負載的歐幾里得範數)。
,則會假設為發散解。非平衡力的歐幾里得範數大於套用負載的歐幾里得範數)。
- 求解方法的排列以 KSTRA 的增加值順序為準。當遇到收斂困難時,程式將會使用次高的策略重新取用新步長。同時會將步長大小縮小至其之前值的四分之一。現在會維持新策略,直到發生更進一步的收斂困難為止,在此情況下,便會選取次高策略,並再次縮小步長大小。
- 程序將會繼續,直到達到步長的最大數目或負載超出允許等級 (這兩個參數都可以由您調整) 為止。
- 當使用高於原始選取策略的任何策略時,將會嘗試恢復至所提供的次低策略:
- 目前策略 (KSTRA = 1、2、3 或 4) 的四個步長並不需要允許迭代數的一半以上,或
- 目前策略 (KSTRA = 5) 已經使用四次。
如果選取的較低策略失敗,則會針對進一步的四個增量使用之前方法,但不會進一步縮小步長大小。
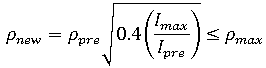
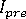 是之前步長中使用的迭代數,
是之前步長中使用的迭代數, 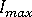 是最大迭代數,
是最大迭代數, 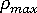 是步長大小限制 (您可以對其進行調整)。例如,假設
是步長大小限制 (您可以對其進行調整)。例如,假設 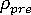 = 1,
= 1, 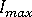 = 20,
= 20, 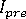 = 4,且
= 4,且 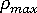 = 2,則我們可以從公式中得出,目前步長大小將是
= 2,則我們可以從公式中得出,目前步長大小將是 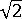 。
。 這也表示在收斂失敗之後,在復原原始步長大小 (亦即在失敗的增量中使用的步長大小) 之前,將會採用每個步長中平均 4 個迭代的步長。請注意,當 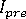 超出
超出 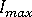 的 40% 時,步長大小將會收縮 (儘管相對較慢)。
的 40% 時,步長大小將會收縮 (儘管相對較慢)。