Le talus de pente d'AutoCAD Civil 3D utilise une technique connue sous le nom de modélisation de représentation des limites de contour ou b-Rep. Pour chaque segment de l'empreinte, une zone de cône, de plan ou de spline délimitée est créée pour correspondre aux paramètres de talus de ce segment. Ces pièces sont sécantes les unes avec les autres, et les pièces résultantes sont associées afin de créer un talus avec une intelligence 3D réelle.
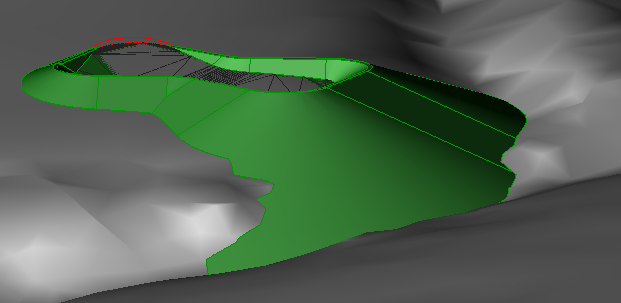
Figure 9 : Angle d'un grand talus de projection
La figure 9 illustre exactement l'intersection avec la surface d'un cône à l'angle extérieur d'un étang. Remarquez que vous ne pouvez pas dessiner de ligne de projection droite, de l'empreinte vers le composant du talus, se poursuivant le long de la vallée dans la partie inférieure gauche. Un algorithme de projection de rayons simple n'intervient pas dans cette partie de la solution, car il ne détecterait que la première intersection de rayons avec la surface, à une altitude plus élevée. En affichant les résultats précis des paramètres de talus, AutoCAD Civil 3D permet aux ingénieurs d'observer les détails importants et d'étudier des options de conception réalistes avec plus de facilité. Par exemple, dans ce cas, nous pouvons constater qu'un mur de soutènement pourrait empêcher le talus de s'affaisser le long de la vallée et ainsi de réviser la conception pour inclure un tel mur.
La recherche d'une solution appropriée devient plus difficile si les segments de talus ne se coupent pas entièrement. AutoCAD Civil 3D utilise des algorithmes de redressement et d'établissement de moyenne pour traiter ces points problématiques et d'autres lors d'un deuxième traitement des calculs par ordinateur. Alors que l'entrée en terre en 2D est relativement claire dans la plupart des cas, la recherche de la solution modifiée en 3D complète peut être beaucoup plus compliquée. Un autre facteur de complication est la précision limitée avec laquelle les ordinateurs peuvent calculer les intersections. Pour ces raisons, les segments courts et les faux angles peuvent être problématiques.