平均要素厚さ
11 番目のユーザ材料定数は、エネルギーベースの劣化で使用する平均要素厚さを定義します。2D 要素では、この値は無視されます。3D (ソリッド)要素の場合、これは材料に関連付けられたソリッド要素の平均厚さとなり、その厚さは要素の層間寸法として定義されます。
「付録 A.5」で説明したように、エネルギー ベースの劣化計算に使用される最終的な有効なひずみは、次の方程式で求めます。
上記の Le は、Abaqus によって定義された代表的な要素の長さです。3D 要素(つまり、ブリック要素と連続体シェル要素)の場合、要素の長さは体積の立方根です。2D 要素(つまり、シェル要素と平面応力要素)の場合、要素の長さは面積の平方根です。
2D 要素の場合、要素の厚さは無視されます。代表的な要素の長さは、要素の面内領域の測定値を提供し、複合材料の層に関連付けるのに役立ちます。ただし、層状ソリッド要素では、代表的な要素の長さが単一の層の測定値に関連付けられていません。ソリッド要素を使用して 2D 要素の結果と比較できるようにするには、層の面内の要素長さの有用な測定値が提供されるように代表的な要素長さを変更する必要があります。
ほとんどの場合、複合材料の破断は単層の平面で発生します。したがって、要素の厚さ方向のサイズを無視する方がより正確になります。これは、ユーザの材料の定義内に提供される平均要素厚さ定数を使用して実行されます。代表的な要素の長さは次のように計算されます。
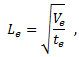
ここで、Ve は要素の体積、te は要素の平均の厚さです。上記の方程式で定義された要素の長さは、ソリッド要素の面内領域の正確な測定値を提供し、ソリッド要素の厚みが一定である場合に、Abaqus が 2D 要素に対して提供する正確な測定値に集約されます。
劣化時間
瞬間的な劣化を使用する Abaqus/Explicit 解析では、材料特性の急速な劣化が、構造の応答に悪影響を与える可能性があります。剛性の変化速度が大きいローカルの材料の応答は、隣接する要素の損傷を時期尚早に開始する材料で衝撃波を生成させる可能性があります。この影響を軽減するには、ユーザ材料定数 11 を使用して材料特性を劣化する期間を指定します。この値はゼロ以上である必要があります。より大きな時間値を設定すると、剛性の変化速度が小さくなります。
破損の開始時には、材料特性は自動的に次の材料の状態には低減しません。材料の剛性は、次の方程式に基づいて更新されます。
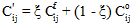
ここで、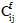
および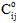 
は、次の材料の状態および以前の状態における材料の剛性をそれぞれ示します。また、
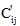は更新された(中間)材料の剛性です。
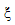は次のように定義されます。
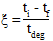
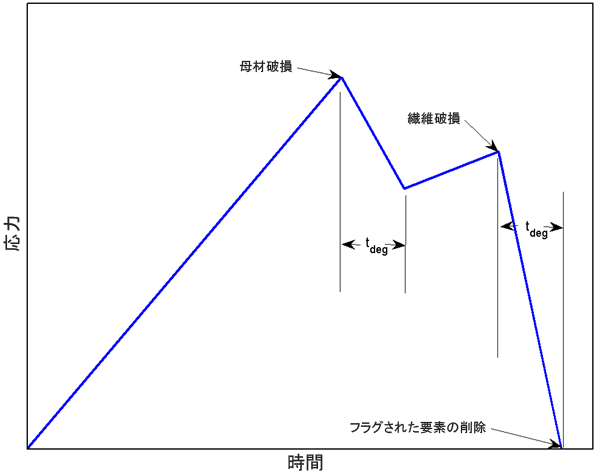
ここで、ti、tf、tdeg は、それぞれ現在の時間、破損開始時間、劣化時間(ユーザ材料定数 11)です。下図は、劣化期間のさまざまな時間値(破損開始後は一定のひずみ)に対する時間の関数としてのローカルの材料応答を示しています。
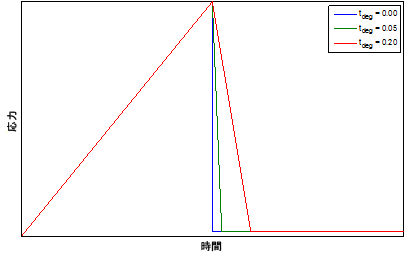
次のプロットは、時間に関して積分点における応力の理想的な例を示しています。
