最后一块复合疲劳拼图将绑定断开率与复合材料的宏观失效链接起来。
损坏演变参数
如上所述，Hansen 和 Baker-Jarvis [36] 通过引入表示微裂纹密度百分比（相对于失效时的微裂纹）的损坏参数 n 将 KTF 与宏观损坏链接起来。损坏变量（表示断裂所需的微裂纹密度的百分比）最初为 0，失效时为 Unity。在其公式中，随时间 t 的推移引入了适用于损坏变量 n 演变的微分表达式，其中损坏变量的演变与绑定断开率直接相关。此方法成功地预测了受各种应力速率影响的聚合物的强度。
这种方法使用了描述 n 演变的微分表达式，与 Hansen 和 Baker-Jarvis 提出的表达式非常相似。
n 0 是通过强制执行条件确定的参数。
ni 是疲劳载荷开始时的损坏值。此公式与 Hansen 和 Baker-Jarvis 的公式之间的差别是，它们的公式假设 λ=1。此值是我们当前实现 2 中使用的默认值。如果 λ=1，
假设 λ 的值为 1.0，然后合并 Eq.57、52 和 56 将提供起始方程用于确定聚合物的疲劳寿命。
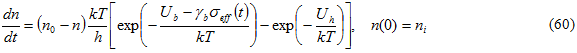
解算 Eq. 61 会随时间推移产生损坏参数演变，这可写为 3 ：
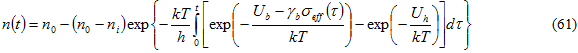
Eq. 61 可以与 Ub、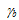
和 Uh 的校准值结合使用来确定损坏参数变为 Unity（即 n = 1）的时间。
2 对于单个线性弹性分析，即没有渐进式失效，选择 λ 无关紧要。λ 的所有求解都将产生相同次数的失效循环。但是，此系数对块载荷和渐进式失效模拟至关重要。
3 我们已假设，在 Eq. 61 中的公式将假设 U 和 T 在疲劳过程中为常数。