动能原理规定:两个连接点之间的压力降对于这两个连接点之间的所有路径都是相同的。动能方程用于计算管网中的压力。
重要: 在每个单元处求解动能原理方程,同时求解每个节点处的连续方程和温度方程,以满足管网解决方案的两个原则。
动能原理方程需要满足这两个连接点之间所有路径的相同压力损失。
对于远离连接节点的任何分支单元的压力降 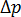 或
或 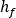 ,通常可以使用体积流动速率函数 Q 表示,如下所示:
,通常可以使用体积流动速率函数 Q 表示,如下所示:
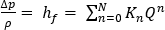
其中,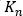 和
和 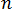 是取决于所使用经验确定的压力降流动速度关系的变量,而 N 是指用于描述压力降的方程顺序。
是取决于所使用经验确定的压力降流动速度关系的变量,而 N 是指用于描述压力降的方程顺序。
该方程对压力添加到管网或对压力从管网中丢失的情况都是有效的。如果对管网增压,例如使用泵时,该压力被视为负压力损失。
注: 除了两个连接点之间的压力降 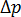 或
或 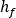 之外,以下因素也会导致压力损失,必须在压力损失计算中予以考虑:
之外,以下因素也会导致压力损失,必须在压力损失计算中予以考虑:
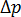 或
或 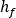 之外,以下因素也会导致压力损失,必须在压力损失计算中予以考虑:
之外,以下因素也会导致压力损失,必须在压力损失计算中予以考虑:
- 因管道壁处的流体剪切引起的摩擦水头损失。此摩擦水头损失在整个长度的管道中始终存在,可在冷却液流动分析中使用 Darcy-Weisbach 方程求解。
- 因液体流的局部影响(如阀、弯头、T 形三连通连接点等)引起的次要损失。
- 加压且被视为负水头损失的泵。
动能原理方程需要表示管网中每一处单元中的压力降关系。
求解每个单元的一般动能原理方程
参考冷却液流动计算域,通常,节点 i 的任何支管单元 j 的压力降关系可表示如下:
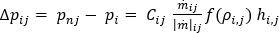
其中, 是源自上述动能原理的压力降流动速率关系,
是源自上述动能原理的压力降流动速率关系,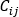 是连接运算符 (+) 或 (-),
是连接运算符 (+) 或 (-),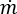 是质量流动速率,而
是质量流动速率,而 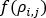 是管网中流体密度的函数。对于不可压缩流体(例如水),这是一个常数。
是管网中流体密度的函数。对于不可压缩流体(例如水),这是一个常数。
注: 使用 Darcy-Weisbach 方程对常规动能原理方程进一步修改,以考虑摩擦水头损失、次要损失和来自泵的负水头损失。
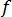 的功能行为完全显示在莫迪图中,这对于可压缩流体和不可压缩流体都是有效的。
的功能行为完全显示在莫迪图中,这对于可压缩流体和不可压缩流体都是有效的。