为了求解冷却回路中的流动，需要计算回路的每个节点上的正确压力以及每个单元中的正确流动速率。
冷却液流动分析基于两个简单原理：
- 连续性原理
- 必须满足整个系统的质量守恒，方法是确保管网中所有连接点的连接点总流入等于该连接点的总流出。除此之外，一系列连接的管道或风管中的总流动速率必须保持不变，无论直径是否有变化都是如此。该原理由连续方程进行描述，将在后续页面中进行介绍。
- 动能原理
- 两个连接点之间的压力降对于这两个连接点之间的所有路径都必须相同。该原理由动能方程进行描述，并可进行修改以包括水头损失、次要损失和回路中存在的任何泵带来的影响。这些引申内容将在后续页面中介绍。
若要求解回路中每个节点上的温度和压力以及每个单元上的流动速率，需要同时求解这些方程。每个方面的引申内容将在后续页面中详细介绍。出现以下方程时应该引起注意，索引 i 指的是管网的节点，索引 j 指的是与该节点连接的单元的分支，如冷却液流动计算域中所述。
流动速率的连续方程
每个节点处都需要满足连续方程：
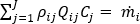适用于 i =1，...节点，j =1....分支单元
其中，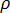
是流体密度，Q 表示管道中的体积流动速率，
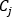是予以考虑节点的给定分支的连接运算符 (+) 或 (-)，如冷却液流动计算域中所述。质量流动速率 
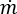= 0（适用于所有内部节点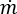）， = 进入或离开管网的质量通量（适用于给定边界节点）。
压力降的动能方程
连接到每个节点的每个支管单元必须满足流动速率压力降关系式，如常规功能原则方程所描述：
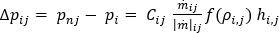
其中，
是源自动能原理方程 
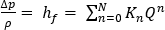的压力降流动速率关系式，
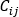是连接运算符 (+) 或 (-)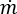， 是质量流动速率，
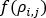是管网中流体密度的函数。对于不可压缩流体（例如水），这是一个常数。
- 包括摩擦水头损失和次要损失
-
但模具冷却回路同时受水头损失和次要损失影响，因此可使用更具体的流动速率压力降关系式。因流体剪切而引起的水头损失是任何直管中流体流动的函数。Darcy-Weisbach 方程计算因管道或风管的直管段长度中摩擦引起的压力降。次要损失是流体流经管件、阀、弯管、弯头、T 形三通、入口、出口、膨胀和收缩而引起的压力损失。可对常规动能原理方程进行修改，以包括摩擦水头损失和次要损失，如下所示：
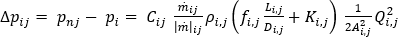
其中，
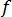是摩擦系数，D 是管道直径，L 是其长度，K 是阻力系数并可从制造商处获得，A 是管道的横截面面积，Q 表示管道中的体积流动速率。
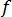也不依赖雷诺数。
- 包括泵
-
当分支具有与它相连的泵或风机单元时，应用的关系式如下所示：
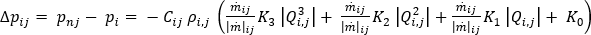
当选择在计算中包括重力时，要在边界节点上考虑高程。默认情况下，此选项处于禁用状态。
温度方程
每个节点处的温度可通过输入该节点的流体总能量获得，如下所示：
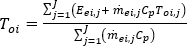
其中，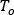
是流体温度，方程右侧指的是分支单元。
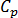是流体的比热，
是到单元 e 的能量传递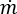， 是该单元中的质量流动速率。