若要以数字方式求解管网中的流动,必须在计算域上使用代数方法表示该管网。
冷却液流动求解方案是一个基于著名的 Patankar 和 Spalding 的简单算法的节点方法。根据图 1 中所示的一系列平行管道,其中连接点 A 处分叉三个分支 1、2 和 3,然后这三个分支在连接点 B 处重新汇聚;出于计算目的,此流动管网必须分解为各个节点和单元。
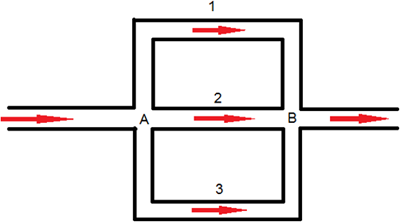
图 1. 经过管网的平行流动
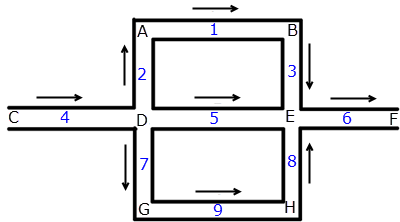
图 2 平行流动管网的计算域
在图 2 中,使用图 1 中所示的相同系列平行管道,节点由字母表示,单元由数字表示。每个单元连接两个节点。观察节点 D,有 4 个分支与它关联。节点 D 通过单元 2、4、5 和 7 连接到节点 A、C、E 和 G。使用代数方法,这可表示为节点 i 通过单元 eij 连接到相邻节点 nij ,其中 j 是与节点 i 相关联的分支数。
连接箭头表明单元的方向。管网中的每个节点具有与其各个分支相关联的连接运算符,该连接运算符确定分支中的流动方向。如果连接箭头指向相应节点,则对相邻节点而言,连接运算符为 (+)。因此,对于节点 D,其中只有 1 个连接运算符指向它,对节点 C 而言只有一个正向连接运算符。其他三个连接运算符都为 (-)。
管网中的每个节点上都需要同时满足连续方程和温度方程。动能原理方程需要表示管网中每个单元上的压力降关系式。