Weiter oben haben wir experimentellen Daten gesehen, wie das Material einen Lastabfall unter Druck zeigt. Bezeichnen wir die Größe dieses Belastungsabfalls als μ. Der Wert von μ variiert je nach Änderung des Belastungswinkels. Daher benötigen wir eine Methode zur Bestimmung von μ für Spannungszustände, die das Druckausfallkriterium auslösen.
0°
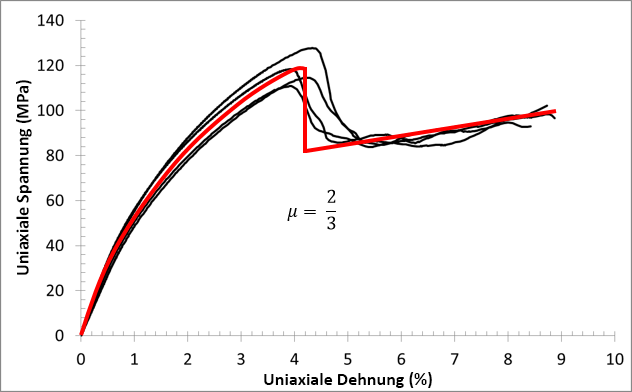
90°
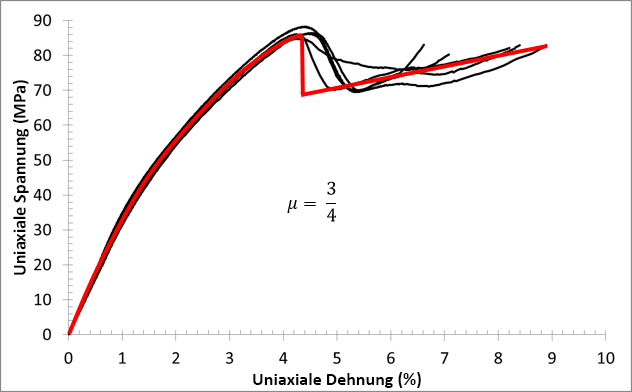
45°
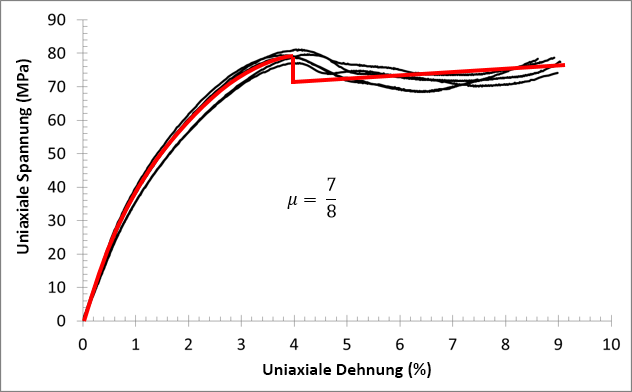
Bestimmen von μ
Im ersten Schritt werden die Hauptspannungen (σI ≥ σII ≥ σIII) und Hauptrichtungen (âI, âII, âIII) des Matrixspannungszustands bestimmt, der das Druckausfallkriterium ausgelöst hat. Die dritte Hauptspannung (σIII) wird immer die Druckspannung mit der größten Größe sein. Als Nächstes bestimmen wir den Winkel zwischen der dritten Hauptrichtung (âIII) und der Hauptmaterialrichtung. Wir bezeichnen diesen Winkel als ξ.
Wir schreiben nun μ als quadratische Funktion des Winkels ξ.
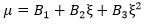
Hierbei werden die Koeffizienten B1, B2 und B3 durch Belastungsabfälle in den drei experimentellen Spannungs-/Dehnungsreaktionen bestimmt. Unter Verwendung der drei bekannten Eingabewinkel ξ (0, 90, 45) und des gemessenen Belastungsabfalls μ für jede Kurve können wir ein Gleichungssystem zur Ermittlung der Koeffizienten B1, B2 und B3 lösen. Diese Koeffizienten werden während der Strukturanalyse verwendet, um den entsprechenden Belastungsabfall zu bestimmen, der für einen beliebigen angegebenen Spannungszustand anzuwenden ist, der das Druckausfallkriterium auslöst.
Die folgende Abbildung zeigt ein Beispiel dafür, wie μ von der Richtung der Hauptdruckspannung in Bezug auf die Hauptfaserausrichtung abhängig ist.
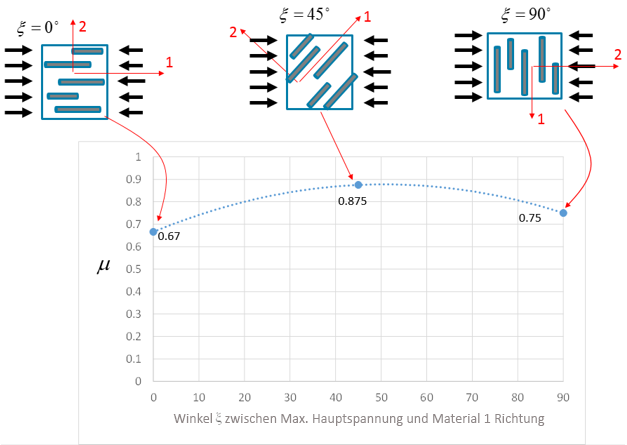
Schadensentwicklung
Nachdem wir μ für den Spannungszustand ermittelt haben, der einen Ausfall auslöst, können wir ihn auf die Spannung des Verbundwerkstoffs anwenden. Die Steifheit des Verbundmaterials wird sofort reduziert, indem die Steifheitsmatrix mit dem Bruch μ multipliziert wird. Nach Anwendung von μ entwickelt sich die Plastizitätsreaktion weiter wie zuvor.