The friction factor,
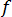, is a component of the Darcy-Weisbach equation, for calculating the head loss due to fluid shear at the pipe of duct wall.
The friction factor,
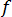, determines the frictional losses in a pipe or duct system, and is dependent upon the equivalent sand grain roughness factor (e/D) of the channel and the Reynolds number, Re, of the fluid flowing through it.
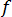is independent of the Reynolds number.
The functional behavior of the dimensionless friction factor,
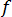, is displayed fully in the Moody diagram, which is valid for both compressible and incompressible fluids. To solve the friction factor numerically, the Moody diagram must be reduced to a form that can be programmed. There are several semi empirical correlation formulae that can be used to reduce the Moody diagram to a programmable form, for different Reynolds number ranges.
Colebrook-White equation
For fully turbulent flow where Re > 4000, the friction factor is accurately represented by the Colebrook-White equation, which combines experimental results of studies of turbulent flow in smooth and rough pipes to a common friction factor:
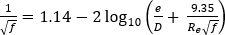
Unfortunately, the equation is implicit in nature and needs to be solved iteratively. For this reason many explicit approximations to the Colebrook-White equation exist along with other expanded forms.
Swamee-Jain equation
The Swamee-Jain equation is the most favored approximation of the implicit Colebrook-White equation, and is the default approximation used for the Coolant Flow analysis. It is given by the equation:
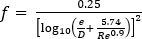
Other equations
Other similar approximations of the Colebrook-White equation that you can select in the software are:
- Haaland
- Serghides
- Altshul
- Evangelides