The work-energy principle states that the pressure drop between two junctions must be the same for all paths between the two junctions. The work-energy equation is used to calculate the pressures in the network.
The work-energy principle equation needs to satisfy the same pressure loss for all the paths between the two junctions.
The pressure drop,
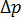 or
or
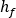 , can be expressed in general terms as a function of the volumetric flow rate, Q, for any branch of elements off a junction node as:
, can be expressed in general terms as a function of the volumetric flow rate, Q, for any branch of elements off a junction node as:
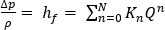
where
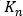 and
and
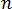 are variables that are dependent on the empirically determined pressure-drop flow-rate relationship used, and N refers to the order of equation used to describe the pressure drop.
are variables that are dependent on the empirically determined pressure-drop flow-rate relationship used, and N refers to the order of equation used to describe the pressure drop.
This equation is valid both for cases where pressure is added to, or lost from, a network. When pressure is added to a network, for example when pumps are used, the pressure is considered to be a negative pressure loss.
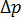 or
or
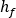 between two junctions, the following also contribute to pressure loss and must be accounted for in the pressure loss calculations:
between two junctions, the following also contribute to pressure loss and must be accounted for in the pressure loss calculations:
- Frictional head loss due to fluid shear at the channel wall. This frictional head loss is always present throughout the length of the channel, and is solved in the Coolant Flow analysis, using the Darcy-Weisbach equation.
- Minor losses, caused by local disruptions of the fluid stream such as valves, bends, tee junctions and the like.
- Pumps, which add pressure and are considered to be negative head loss.
The work-energy principle equation needs to represent the pressure drop relationship in every element in the network.
Solving the general work energy principle equation for each element
Referring to the coolant flow computational domain, in general the pressure drop relationship for any of the branch elements j of node i can be expressed as:
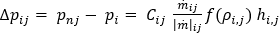
where
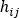 is the pressure drop flow rate relationship derived from the work energy principle above,
is the pressure drop flow rate relationship derived from the work energy principle above,
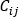 is the connectivity operator, (+) or (-),
is the connectivity operator, (+) or (-),
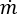 is the mass flow rate, and
is the mass flow rate, and
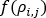 is a function of the density of the fluid in the network. For incompressible fluids, such as water, this is a constant.
is a function of the density of the fluid in the network. For incompressible fluids, such as water, this is a constant.
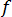 , is displayed fully in the Moody diagram, which is valid for both compressible and incompressible fluids.
, is displayed fully in the Moody diagram, which is valid for both compressible and incompressible fluids.