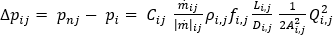ダルシー ワイスバッハの式では、配管またはダクトの直線長さにおける摩擦を原因とする圧力降下を計算します。
配管またはダクト内の摩擦損失水頭を求める際、基本的に最も安全で多機能な式となるのが、ダルシー ワイスバッハの式です。
ダルシー ワイスバッハの式は次で与えられます。
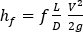
ここで、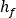
は圧力損失(メートル)、
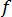は摩擦係数、V は冷却管の平均流速、D は冷却管の直径、L は冷却管の長さ、
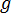は重力加速度です。
無次元の摩擦係数 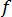の機能的な挙動は、ムーディ線図に詳しく示されています。これは、圧縮性の流体と非圧縮性の流体の両方で有効です。摩擦係数を数値的に解析するには、コールブルック ホワイトの式のスワミー ジャイン近似などの近似式を使用して、ムーディ線図をプログラム可能な形式にまで縮小する必要があります。
ダルシー ワイスバッハの式を仕事-エネルギー定理方程式に関連付けるには、次のように、ダルシー ワイスバッハの式を体積流量の観点から記述し直す必要があります。
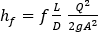
そして、高さではなく圧力の観点から記述します。
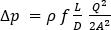
再び仕事-エネルギー定理方程式を基に、計算領域内の各要素について摩擦損失水頭を式に追加した後、ダルシー ワイスバッハの式の離散形式を次のように記述することができます。
