仕事-エネルギーの定理は、2 つの接合点間の圧力降下が、2 つの接合点間のすべての経路で同じでなければならないことを述べています。仕事-エネルギー方程式は、ネットワーク内の圧力の計算に使用します。
重要: 仕事-エネルギー方程式は、各ノードでの連続方程式および各ノードでの温度方程式と同時に各要素で計算され、ネットワーク解析の 2 つの原則を満たします。
仕事-エネルギー定理方程式では、2 つの接合点間のすべての経路で同じ圧力損失を満たす必要があります。
圧力降下 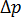 または
または 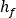 は、一般に、接合ノードから離れた要素の任意の分岐における体積流量 Q の関数として次のように表すことができます。
は、一般に、接合ノードから離れた要素の任意の分岐における体積流量 Q の関数として次のように表すことができます。
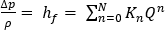
この式の 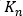 と
と 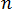 は、ここで使用する、経験的に決定された圧力降下-流量関係に依存する変数です。N は、圧力降下の記述に使用する方程式の次数です。
は、ここで使用する、経験的に決定された圧力降下-流量関係に依存する変数です。N は、圧力降下の記述に使用する方程式の次数です。
この方程式は、ネットワークへの加圧の場合にもネットワークからの減圧の場合にも有効です。ネットワークに加圧する場合(ポンプを使用する場合など)は、圧力は負の圧力損失であると見なされます。
注: 2 つの接合点間の圧力降下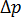 または
または 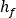 に加えて、次のものも圧力損失に影響を与えるため、圧力損失を計算する際に考慮する必要があります。
に加えて、次のものも圧力損失に影響を与えるため、圧力損失を計算する際に考慮する必要があります。
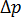 または
または 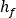 に加えて、次のものも圧力損失に影響を与えるため、圧力損失を計算する際に考慮する必要があります。
に加えて、次のものも圧力損失に影響を与えるため、圧力損失を計算する際に考慮する必要があります。
- 摩擦損失水頭。冷却管壁で生じる流体せん断が原因で発生します。この摩擦損失水頭は冷却管の長さ全体で常に存在し、冷媒流解析ではダルシー ワイスバッハの式を使用して解析します。
- マイナー損失。バルブ、ベンド、T 型接合点などの流体ストリームの局部的崩壊が原因で発生します。
- ポンプ。圧力を加えるもので、負の損失水頭と見なされます。
仕事-エネルギー定理方程式では、ネットワーク内のすべての要素における圧力降下の関係を表現する必要があります。
各要素における一般の仕事-エネルギー定理方程式の解析
冷媒流の計算領域を基に、ノード i の任意の分岐要素 j における圧力降下関係は、一般に次のように表すことができます。
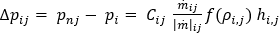
ここで、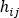 は前述の仕事-エネルギーの定理から派生した圧力降下-流量関係、
は前述の仕事-エネルギーの定理から派生した圧力降下-流量関係、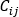 は接続演算子(+)または(-)、
は接続演算子(+)または(-)、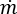 は質量流量、
は質量流量、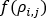 はネットワーク内の流体の密度関数です。水などの非圧縮性流体では、これは定数になります。
はネットワーク内の流体の密度関数です。水などの非圧縮性流体では、これは定数になります。
注: 一般の仕事-エネルギー定理方程式はさらに、ダルシー ワイスバッハの式を使用して修正され、摩擦損失水頭、マイナー損失、ポンプからの負の損失水頭が考慮されます。
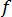 の機能的な挙動は、ムーディ線図に詳しく示されています。これは、圧縮性の流体と非圧縮性の流体の両方で有効です。
の機能的な挙動は、ムーディ線図に詳しく示されています。これは、圧縮性の流体と非圧縮性の流体の両方で有効です。