連続方程式は、流路ネットワーク内の流量の計算に使用します。
一般に、流体密度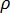 
は流体の温度および圧力の変化に応じて変動する場合があります。サーフェス S で囲まれた固定のコントロール ボリューム 
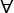では、質量保存の一般的な記述は次のように与えられます。
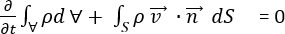
ここで、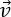
は点における速度、
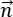はサーフェス S に対する外向きの単位法線ベクトル、
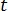は時間です。
1 つ目の項は、コントロール ボリュームでの時間経過による質量の累積を表します。定常状態の流れでは、1 つ目の項は次のようになります。
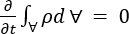
サーフェス点では、内積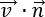 
によって、サーフェスを横切る速度の成分が与えられます。したがって、2 つ目の項では、コントロール ボリュームのサーフェス全体にわたる流体の正味流出が得られます。
連続方程式
配管またはダクト内における流体の定常状態での圧縮性流動では、質量の保存のことを連続の定理と呼び、連続方程式において、配管またはダクトの任意の断面領域 A における流体の密度 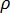と流体の平均速度 V との積として次のように記述することができます。
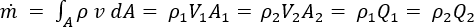
ここで、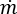
は配管またはダクトを流れる質量流出で、Q は配管またはダクト内の体積流量を表します。
連続方程式はネットワーク内のすべてのノードで満たされる必要があります。
各ノードにおける連続方程式の計算
冷媒流の計算領域を基に、連続方程式は各内部ノードで次のように代数的に表現できます。
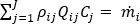ただし i =1...ノード数、j =1....分岐要素数
ここで、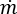 はすべての内部ノードで 0 となります。 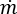は、与えられた境界ノードでネットワークを流入または流出する質量流束になります。
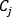は、対象となるノードの与えられた分岐に対する接続演算子(+)または(-)です。