冷却回路内の流れを解析するためには、各ノードでの正しい圧力と、回路の各要素における正しい流量を計算する必要があります。
冷媒流解析は 2 つの単純な定理に基づいています。
- 連続の定理
- 系全体で質量の保存を満たす必要があります。それには、ネットワーク内のすべての接合点について、接合点に流入する総流量と、接合点から流出する総流量とを等しくする必要があります。これに加えて、直列に接続された配管またはダクト内では、直径の変更に関係なく、総流量が一定のままである必要があります。この定理は連続方程式により記述されます。以降のページでこの定理について説明します。
- 仕事-エネルギーの定理
- 2 つの接合点間の圧力降下が、2 つの接合点間のすべての経路で同じである必要があります。この定理は仕事-エネルギーの方程式により記述され、回路に存在する損失水頭、マイナー損失、およびすべてのポンプの影響を含めるように修正されます。以降のページでこれらの導出について説明します。
回路内の各ノードの温度と圧力、および各要素の流量を解析するためには、これらの方程式を同時に解析する必要があります。以降のページでそれぞれの導出について詳しく説明します。次の方程式で、添え字 i はネットワークのノードを表し、添え字 j はノードに接続している要素の分岐を表します(「冷媒流の計算領域」を参照)。
流量の場合の連続方程式
各ノードで連続方程式を満たす必要があります。
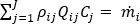ただし i =1...ノード数、j =1....分岐要素数
ここで、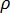
は流体の密度、Q は流路内の体積流量、
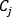は対象となるノードの与えられた分岐に対する接続演算子(+)または(-)を表します(「冷媒流の計算領域」を参照)。
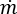は質量流量で、すべての内部ノードで 0 となります。 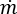は、与えられた境界ノードでネットワークを流入または流出する質量流束です。
圧力降下の場合の仕事-エネルギーの方程式
次の一般の仕事-エネルギー定理方程式に示すように、各ノードに接続しているそれぞれの分岐要素で、流量-圧力降下関係を満たす必要があります。
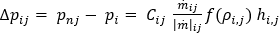
ここで、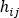
は仕事-エネルギー定理方程式 
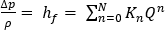から派生した圧力降下-流量関係、
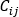は接続演算子(+)または(-)、 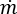は質量流量、
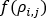はネットワーク内の流体の密度関数です。水などの非圧縮性流体では、これは定数になります。
- 摩擦損失水頭とマイナー損失を含める
-
ただし、金型の冷却回路は損失水頭とマイナー損失の両方の影響を受けるため、より具体的な流量-圧力降下関係が使用されます。流体せん断を原因とする損失水頭は、任意の直線配管内の流体の関数です。ダルシー ワイスバッハの式では、配管またはダクトの直線長さにおける摩擦を原因とする圧力降下を計算します。マイナー損失は、継手、バルブ、ベンド、エルボ、ティー、流入口、流出口、拡流部、縮流部を流れる流体を原因とする圧力損失です。次のように、摩擦損失水頭とマイナー損失を含めるように、一般の仕事-エネルギー定理方程式を修正することができます。
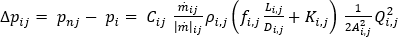
ここで、
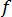は摩擦係数、D は流路の直径、L は流路の長さ、K は抵抗係数で、製造元から取得できます。A は流路の断面積、Q は流路内の体積流量を表します。
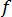もレイノルズ数に依存しません。
- ポンプを含める
-
分岐にポンプまたはファン要素が接続されている場合、適用される関係は次のようになります。
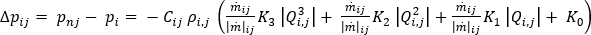
計算に重力を含めた場合は、境界ノードで高さが考慮されます。既定では、オフに設定されています。
温度の方程式
各ノードの温度は、そのノードに流入する流体の全エネルギーから取得され、次で与えられます。
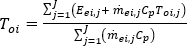
ここで、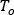
は流体の温度で、方程式の右辺は分岐要素を表します。
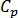は流体の具体的な熱量、
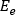は要素 e へのエネルギー伝達、 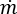は要素内の質量流量です。