ネットワーク内の流れを数値で解析するには、ネットワークを計算領域上で代数的に表現する必要があります。
冷媒流解析の仕組みはノード法であり、Patankar と Spalding によるよく知られた SIMPLE アルゴリズムに基づいています。図 1 に示すように、1 組の並列の冷却管において、1、2、3 の 3 つの分岐があり、接合点 A で発散し、接合点 B で再び発散する場合、このフロー ネットワークを計算上の目的でノードと要素に分割する必要があります。
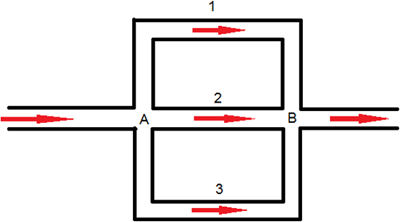
図 1. ネットワークを流れる並列の流れ
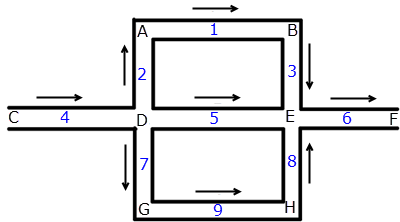
図 2. 並列の流れのネットワークにおける計算領域
図 2 でも 図 1 と同じ 1 組の並列の冷却管を使用していますが、ノードを文字で表現し、要素を番号で表現しています。要素はそれぞれ 2 つのノードを結合しています。たとえばノード D を見てみましょう。このノードには 4 つの分岐が関連付けられています。ノード D は、要素 2、4、5、7 を通じてノード A、C、E、G に接続しています。代数的には、ノード i が要素 eij を通じて隣接するノード nij に接続していると表現できます。ここで、j はノード i に関連付けられている分岐の数です。
接続の矢印は、要素の方向を示しています。ネットワーク内のすべてのノードで、接続演算子がノードの各分岐に関連付けられており、分岐での流れの方向を決定します。接続の矢印がノードを向いている場合、接続演算子は隣接するノードに対して(+)になります。たとえばノード D では、ノード D に向かう接続演算子は 1 つしかなく、ノード C に対する正の接続演算子のみです。他の 3 つの接続演算子はすべて(-)です。
ネットワーク内のすべてのノードで、連続方程式と温度方程式の両方を満たす必要があります。仕事-エネルギー定理方程式では、ネットワーク内のすべての要素における圧力降下の関係を表現する必要があります。