한 표면과 인접한 표면 사이의 각도가 0도나 180도에 매우 가까운 4면체 요소를 면 사이의 각도가 매우 큰 4면체라고 합니다.
끼인 각이 매우 큰 4면체가 3D 메쉬 수정 마법사: 
()에서 탐지되었습니다.
설명
모델의 수학적 해석은 메쉬 요소가 균등한 정4면체라는 가정을 기반으로 합니다. 실제로 메쉬 4면체는 이상적인 정4면체부터 심하게 왜곡되어 결과에 부정적인 영향을 미치는 4면체에 이르기까지 다양합니다. 따라서 뒤틀린 4면체 수를 최대한 줄여야 합니다. 종횡비는 메쉬 품질을 측정하는 데 가장 일반적으로 사용되는 방법입니다. 다른 방법으로는 내부의 긴 모서리 및 종횡비가 높은 4면체가 있습니다.
위 다이어그램에서 절점 A와 D가 서로 가까이 있으면 면 ABC와 BCD 사이의 각도가 0에 가까워집니다. 이 4면체의 경우 끼인 각이 매우 작습니다. 진단을 위해 2도보다 작은 기본 임계값을 극값으로 간주합니다.
또는 아래 다이어그램에서 면 ABC와 ACD 사이의 각도가 180도에 가까우면 납작한 4면체가 생성됩니다. 이 4면체의 경우 끼인 각이 매우 큰 것으로 간주됩니다. 진단을 위해 기본 임계값을 178도로 간주합니다.
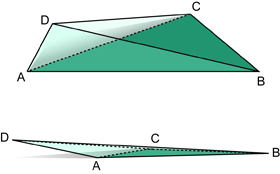
해석에 대한 영향
끼인 각이 큰 4면체로 인해 왜곡된 결과가 발생할 수 있습니다. 예를 들어 한 절점의 온도는 해당 절점이 연결된 모든 절점의 온도를 고려합니다. 위 다이어그램에서 유동은 오른쪽에서 왼쪽으로 흐르고 목표는 절점 D의 온도를 예측하는 것이라고 가정합니다. 아래 다이어그램에서 B와 D 사이의 거리가 더 크기 때문에 B의 온도 기여도가 모든 계산에서 과장됩니다.
권장 조치
3D 메쉬 수정 마법사, ()에서 이 문제를 대부분 해결할 수 있습니다. 수천 개의 4면체를 수정해야 하는 경우 약간의 시간이 걸릴 수 있습니다.