En fonction de la géométrie du modèle, vous serez amené à insérer une ou plusieurs contraintes afin de définir la forme ou la taille du modèle. Les contraintes mettent en place les règles que le modèle doit suivre. Contraindre un modèle revient à contrôler les modifications possibles de sa forme ou de sa taille, c'est-à-dire ses "degrés de liberté". Par exemple, un cercle possède deux degrés de liberté : l'emplacement de son centre et la valeur de son diamètre. Si le centre et le diamètre sont spécifiés, le cercle est entièrement contraint : la gestion de ces valeurs est alors possible. Les contraintes spécifient les relations unissant les fonctions géométriques (par exemple, deux fonctions sont perpendiculaires, parallèles, tangentes, concentriques ou possèdent le même milieu ou un même rayon).
Les contraintes sont liées aux cotes pour la gestion de la forme et de la taille du modèle. Chaque fois que vous modifiez le modèle, la géométrie conserve les relations entre les objets en fonction des contraintes appliquées. En ajoutant des contraintes, vous précisez l'intention de la conception. Ainsi, il est possible de mettre en oeuvre une contrainte parallèle entre deux lignes sur la base de la géométrie du modèle. Vous pourriez également ajouter une contrainte pour imposer la même longueur aux deux lignes.
Tandis que vous appliquez des contraintes géométriques, continuez à analyser le modèle, en vérifiant et en remplaçant les contraintes comme il convient. Plus vous gagnerez de l'expérience, plus vous serez en mesure d'identifier les contraintes gérant le modèle afin de répondre à vos besoins de conception. Certaines contraintes s'appliquent uniquement aux lignes, d'autres aux arcs, aux cercles ou aux points uniquement.
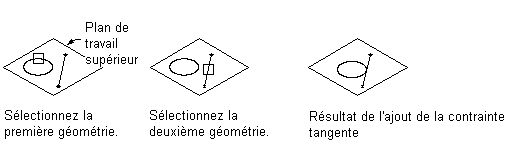
Application d'une contrainte de tangente
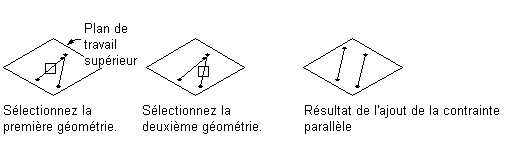
Application d'une contrainte parallèle
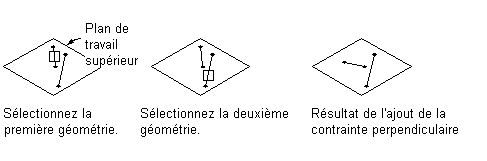
Application d'une contrainte perpendiculaire
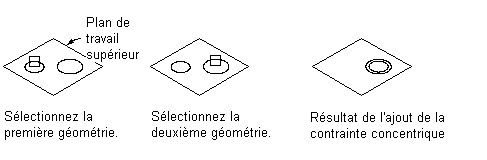
Application d'une contrainte concentrique
Le générateur de contenu propose un éventail de dix contraintes géométriques. La liste suivante décrit ces contraintes et les fonctions auxquelles elles sont associées.
- Tangente
-
Définie entre la géométrie incurvée (tel un cercle ou un arc) et une autre géométrie incurvée ou une ligne. Cette contrainte rend deux courbes tangentielles l'une par rapport à l'autre, même si elles ne partagent pas physiquement un point. La tangence est couramment utilisée en tant que contrainte d'une ligne à un arc ou à un cercle.
- Parallèle
-
Peut être définie pour des paires de géométries ayant une direction (des lignes, par exemple). Rend deux lignes, ou davantage, parallèles entre elles.
- Perpendiculaire
-
Peut être définie entre des paires de géométries avec une direction, telles que des lignes. Cette contrainte place les lignes sélectionnées à angle droit.
- Concentrique
-
Peut être définie pour toute combinaison de cercles et de points. Cette contrainte fixe les centres de la géométrie au même emplacement. Les utilisations courantes incluent notamment le cercle à cercle (le centre des deux cercles est le même), le cercle à point (le point se situe au centre du cercle) et le point à point (les points sont les mêmes).
- Coïncidence
-
Peut être définie entre un point et toute géométrie. Place deux points (centres compris) au même emplacement ; le point fait partie de la géométrie.
- Distance identique
-
Peut être définie entre deux paires de géométries. La distance entre la première paire de géométries est fixée à la même distance de la deuxième paire. La contrainte de distance identique ne contrôle pas la distance réelle. Chaque paire de géométries doit correspondre à l'une des configurations suivantes : toute combinaison de points et de lignes, deux cercles et deux arcs concentriques contraints ou encore un point et un cercle/un arc liés par une contrainte concentrique.
- Rayon identique
-
Peut être défini entre 2 cercles ou 2 arcs. Attribue la même valeur au rayon de deux cercles ou arcs. Les contraintes de rayon égal ne contrôlent pas la valeur des rayons.
- Milieu
-
Peut être défini entre un point et deux autres points ou deux autres lignes. Le point se trouve à égale distance des deux autres géométries. Les contraintes de milieu ne contrôlent pas la distance. La contrainte d'un point au milieu d'une ligne fait partie des utilisations courantes.
- Symétrie
-
Peut être définie entre deux géométries de même type et une ligne. Les deux géométries sont organisées de manière symétrique des deux côtés de la ligne. La contrainte de symétrie n'oblige pas la géométrie contrainte à conserver une image miroir exacte.
- Perpendiculaire
-
Peut être définie entre une ligne ou une courbe et une courbe. Notez que la normale ne peut pas s'appliquer à deux lignes. Préférez dans ce cas la contrainte perpendiculaire. Les courbes se coupent et les directions des tangentes aux courbes sont perpendiculaires au point d'intersection. La contrainte d'une ligne au niveau de la perpendiculaire d'une ellipse fait partie des utilisations courantes.