In der Welt der traditionellen Zeichnungsentwürfe gab es keine NURBS-Kurven und -Oberflächen. Sie wurden speziell für computergestütztes 3D-Modellieren entwickelt. Kurven und Oberflächen stellen Konturlinien oder Konturen innerhalb eines dreidimensionalen Modellierraums dar. Sie sind mathematisch aufgebaut.
Die NURBS-Mathematik ist komplex, und dieser Abschnitt stellt nur eine Einführung in einige NURBS-Konzepte dar, die Ihnen vermittelt, was Sie erstellen, und warum NURBS-Objekte sich so verhalten, wie sie es tun. Eine umfassende Beschreibung der Mathematik und Algorithmen in der NURBS-Modellierung finden Sie in The NURBS Book von Les Piegl und Wayne Tiller (New York: Springer, zweite Ausgabe 1997).
Definition und Parameterraum
Der Begriff NURBS ist ein Akronym für Non-Uniform Rational B-Splines, also nicht gleichförmige, rationale B-Splines. Bedeutung der einzelnen Begriffe:
- Non-Uniform (nicht gleichmäßig) bedeutet, dass der Einflussbereich eines Kontrollscheitelpunkts variieren kann. Dies ist besonders beim Modellieren unregelmäßiger Oberflächen nützlich.
- Rational bedeutet, dass die zum Darstellen der Kurve oder Oberfläche verwendete Gleichung als Verhältnis von zwei Polynomen und nicht durch ein einzelnes Summenpolynom ausgedrückt wird. Die rationale Gleichung bietet ein besseres Modell einiger wichtiger Kurven und Oberflächen, vor allem konischer Querschnitte, Kegel, Kugeln und so weiter.
- Ein B-Spline (für Basis-Spline) ist eine Möglichkeit, eine zwischen drei oder mehr Punkten interpolierte Kurve zu erstellen.
Mit dem Hilfsmittel "Linie" und anderen Kontur-Hilfsmitteln erstellte Kontur-Kurven sind Bezier-Kurven, eine spezielle Version von B-Splines.
Die Eigenschaft "Nicht gleichmäßig" von NURBS-Objekten hat entscheidende Auswirkungen. Da sie mathematisch generiert werden, verfügen NURBS-Objekte zusätzlich zum dreidimensionalen geometrischen Raum, in dem Sie angezeigt werden, über einen Parameterraum. Insbesondere gibt eine Gruppe von Werten, die als Knoten bezeichnet werden, den Einflussbereich jedes Kontrollscheitelpunkts (KS) auf der Kurve oder Oberfläche an. Knoten sind im dreidimensionalen Raum unsichtbar, und Sie können sie nicht direkt manipulieren. Gelegentlich beeinflusst ihr Verhalten jedoch die Darstellungsweise des NURBS-Objekts. Auf diese Situationen wird in diesem Thema hingewiesen. Der Parameterraum ist eindimensional für Kurven, die über eine einzige topologische U-Dimension verfügen, obwohl sie geometrisch im dreidimensionalen Raum bestehen. Oberflächen besitzen zwei Dimensionen im Parameterraum, die als U und V bezeichnet werden.
NURBS-Kurven und -Oberflächen ändern sich bei den geometrischen affinen Standardtransformationen (Transformationen) oder bei Perspektiv-Projektionen nicht. Die KS steuern das Objekt lokal, d. h. das Verschieben eines KS oder das Ändern seiner Gewichtung beeinflusst das Objekt nicht über die benachbarten KS hinaus. (Sie können diese Eigenschaft überschreiben, indem Sie die Funktion "Weiche Auswahl" verwenden.) Außerdem umgibt das Steuergitter, das die KS verbindet, die Oberfläche. Diese Eigenschaft wird als konvexe Hülle bezeichnet.
Grad und Kontinuität
Alle Kurven haben einen Grad. Der Grad einer Kurve ist der höchste Exponent in der zum Darstellen der Kurve verwendeten Gleichung. Eine lineare Gleichung ist eine Gleichung ersten Grades, eine quadratische Gleichung eine Gleichung zweiten Grades. NURBS-Kurven werden normalerweise druch kubische Gleichungen dritten Grades repräsentiert. Höhere Grade sind möglich, aber normalerweise unnötig.
Kurven sind außerdem durch Kontinuität gekennzeichnet. Eine kontinuierliche Kurve ist ununterbrochen. Es gibt verschiedene Kontinuitätsstufen. Eine Kurve mit einem Winkel (einer Spitze) ist C 0 -kontinuierlich, d. h. die Kurve ist ununterbrochen, hat an der Spitze aber keine Ableitung. Eine Kurve ohne solche Spitzen, deren Krümmung sich aber ändert, ist C 1 -kontinuierlich. Ihre Ableitung ist auch kontinuierlich, ihre zweite Ableitung hingegen nicht. Eine Kurve mit ununterbrochener, nicht veränderter Krümmung hat die Kontinuitätsstufe C 2 . Sowohl ihre erste als auch ihre zweite Ableitung sind ebenfalls kontinuierlich.

Stufen der Kurvenkontinuität:
Links: C 0 , aufgrund des Winkels an der Spitze.
Mitte: C 1 , an der Spitze ist ein Halbkreis mit einem kleineren Halbkreis verbunden.
Rechts: C 2 , der Unterschied ist nur geringfügig, aber die rechte Seite ist nicht halbkreisförmig und verschmilzt mit der linken.
Eine Kurve kann noch höhere Ebenen von Kontinuität aufweisen, für computergestütztes Modellieren reichen diese drei jedoch völlig aus. Mit dem bloßen Auge ist der Unterschied zwischen einer Kurve der Kontinuitätskurve C2 und einer mit höherer Kontinuität nicht erkennbar.
Kontinuität und Grad sind voneinander abhängig. Eine Gleichung dritten Grades kann eine Kurve der Kontinuitätsstufe C 2 generieren. Daher werden Kurven höheren Grads bei der NURBS-Modellierung im Allgemeinen nicht benötigt. Kurven höheren Grads sind zudem numerisch weniger stabil; daher wird ihre Verwendung nicht empfohlen.
Verschiedene Segmente einer NURBS-Kurve können unterschiedliche Ebenen von Kontinuität aufweisen. Sie können die Kontinuitätsebene insbesondere durch das platzieren von KS am gleichen Ort oder sehr nah beieinander senken. Zwei übereinanderliegende KS schärfen die Krümmung. Drei übereinanderliegende KS erstellen eine winklige Spitze in der Kurve. Diese Eigenschaft von NURBS-Kurven wird als Einflussverstärkung bezeichnet. Praktisch wird in diesem Bereich der Kurve der Einfluss der zusätzlichen ein oder zwei KS kombiniert.
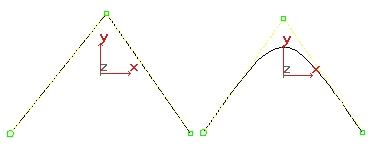
Auswirkungen der Einflussverstärkung: Es befinden sich drei KS auf dem linken Gipfel, zwei auf dem rechten.
Durch Verschieben eines der KS vom anderen KS weg erhöhen Sie die Kontinuitätsebene der Kurve wieder. Die Einflussverstärkung wird zudem beim Verschmelzen von KS angewendet. Verschmolzene KS erstellen eine schärfere Krümmung oder Spitze in der Kurve. Dieser Effekt wird aufgehoben, wenn Sie die KS trennen und voneinander wegschieben.
Der Grad, die Kontinuität und die Einflussverstärkung gelten ebenso für NURBS-Oberflächen wie für Kurven.
Filtern von Kurven und Oberflächen
Durch das Filtern einer NURBS-Kurve werden mehr KS hinzugefügt. Durch Filtern erhalten Sie bessere Steuerungsmöglichkeiten über die Form der Kurve. Wenn Sie eine NURBS-Kurve verfeinern, behält 3ds Max die Originalkrümmung bei. Mit anderen Worten, die Form der Kurve ändert sich nicht, aber die benachbarten KS entfernen sich vom KS, den Sie hinzufügen. Dies ist wegen der Vielfältigkeit: Würden sich die benachbarten KS nicht bewegen, würde die höhere Anzahl der KS die Kurve schärfen. Um diesen Effekt zu vermeiden, filtern Sie die Kurve zunächst und transformieren dann die neu hinzugefügten KS oder passen ihre Gewichtungen an.
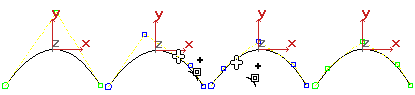
Filtern einer NURBS-Kurve
NURBS-Oberflächen haben im Wesentlichen die gleichen Eigenschaften wie NURBS-Kurven, die von einem eindimensionalen Parameterraum auf zwei Dimensionen erweitert werden.
Neubestimmen der Parameter von KS-Kurven und -Oberflächen
Wenn Sie eine NURBS-Kurve oder -Oberfläche filtern, empfiehlt es sich, die Parameter neu zu bestimmen. Durch die Neubestimmung der Parameter wird der Parameterraum angepasst, damit die Kurve bzw. Oberfläche sich bei einer Bearbeitung in Ansichtsfenstern korrekt verhält. Es gibt zwei Möglichkeiten für das Erstellen neuer Parameter:
- Sehnenlänge
Durch Neubestimmung der Parameter nach Sehnenlänge werden Knoten im Parameterraum anhand der Quadratwurzel der Länge der einzelnen Kurvensegmente angeordnet.
- Gleichmäßig
Bei der gleichmäßigen Neubestimmung der Parameter werden die Knoten gleichmäßig angeordnet. Ein gleichmäßiger Knotenvektor hat den Vorteil, dass die Kurve oder Oberfläche nur lokal verändert wird, wenn Sie sie bearbeiten.
Bei KS-Kurven- und KS-Oberflächen-Unterobjekten haben Sie die Möglichkeit, die Parameter automatisch neu bestimmen zu lassen, wenn Sie die Kurve oder Oberfläche bearbeitet haben.
Konzepte für Punktkurven und -oberflächen
Sie können auf die gleiche Weise mit Punktkurven und Punktflächen arbeiten wie mit KS-Kurven und KS-Oberflächen. Die Punkte, die diese Objekte steuern, müssen auf der Kurve oder Oberfläche liegen. Es gibt kein Steuergitter und keine Gewichtungssteuerung. Hierbei handelt es sich um eine einfachere Benutzeroberfläche, die häufig aufgrund des Bedienkomforts bevorzugt wird. Mit punktgestützten Objekten können Sie außerdem Kurven erstellen, die auf abhängigen (beschränkten) Punkten basieren, und sie anschließend zum Erstellen abhängiger Oberflächen verwenden.
Sie können sich Punktkurven und -oberflächen als eine Schnittstelle zu KS-Kurven und KS-Oberflächen vorstellen, die die vollständig definierten NURBS-Objekte sind. Die zugrundeliegende Darstellung der Kurve bzw. Oberfläche wird weiterhin mithilfe von KS erstellt.
Sie können sich eine Punktkurve oder -oberfläche auch als von ihren Punkten abhängig vorstellen. Mithilfe der Schaltfläche "Kurve umwandeln" können Sie eine Punktkurve oder -oberfläche in eine KS-Kurve bzw. -Oberfläche ändern und umgekehrt.