Nachdem Sie diese Optionen festgelegt haben, wirken sie sich so lange auf Dynamische Simulation aus, bis sie wieder geändert werden. Legen Sie die Optionen unmittelbar nach dem Öffnen der dynamischen Simulation fest.
- Klicken Sie in der Multifunktionsleiste auf Registerkarte Umgebungen
Gruppe Beginnen
Dynamische Simulation, um die Gruppen der dynamischen Simulation einzublenden.
- Registerkarte Dynamische Simulation
Gruppe Verwalten
Simulationseinstellungen
- Klicken Sie auf Abhängigkeiten automatisch in Normverbindungen umwandeln, um den automatischen Converter für die dynamische Simulation (Constraint Reduction Engine oder CRE) zu aktivieren.
In der Standardeinstellung ist der Translator aktiviert.
Wenn Sie auf OK klicken, wandelt die CRE Baugruppenabhängigkeiten automatisch in Norm gelenke um und aktualisiert umgewandelte Gelenke, wenn Sie diesen Mechanismus das nächste Mal öffnen.
- Wenn bei Überbestimmung eines Mechanismus eine Warnung ausgegeben werden soll, wählen Sie die Option Warnung bei überbestimmtem Mechanismus.
Dies ist zwar die Standardeinstellung für neue Mechanismen, aber dies ist nicht vorgabegemäß für Mechanismen, die mit Versionen vor 2008 erstellt wurden, aktiviert. Wenn Sie diese Option aktivieren und der Mechanismus überbestimmt ist, gibt die Software eine Meldung aus, sobald Sie auf OK klicken und bevor die Normverbindungen automatisch erstellt werden.
- Wenn Sie die Komponenten in den verschiedenen beweglichen Gruppen visuell kennzeichnen möchten, aktivieren Sie das Kontrollkästchen Bewegliche Gruppen farblich hervorheben. Vorab definierte Farbüberschreibungen werden den Komponenten in der gleichen beweglichen Gruppe zugewiesen. Mit dieser Option können Sie die Beziehungen der Komponenten zueinander analysieren. Um die Komponenten wieder in der vorgabegemäß zugewiesen Farbe anzuzeigen, deaktivieren Sie das Kontrollkästchen im Dialogfeld Einstellungen, oder klicken Sie mit der rechten Maustaste auf den Knoten Bewegliche Gruppen, und wählen Sie die Option Bewegliche Gruppen farblich hervorheben.
- Klicken Sie auf Alle Anfangspositionen bei 0.0
, wenn Sie alle Anfangspositionen des Freiheitsgrads (FHG) auf 0 setzen möchten, ohne die tatsächliche Position des Mechanismus zu ändern.
Verwenden Sie diese Option, wenn Sie im Ausgabediagramm variable Plots mit dem Ausgangspunkt 0 anzeigen möchten.
- Klicken Sie auf Alles zurücksetzen
, um alle
Koordinatensysteme auf die während der Konstruktion des Gelenkkoordinatensystems angegebenen Anfangspositionen zurückzusetzen.
Dies ist die Standardeinstellung.
- Klicken Sie auf
AIP-Belastungsanalyse , um alle FEM-Informationen zur Analyse mit der AIP-Belastungsanalyse vorzubereiten.
Dadurch werden die FEM-relevanten Daten in den Bauteildateien der ausgewählten Bauteile gespeichert.
- Klicken Sie ansonsten auf
ANSYS-Simulation , um eine Datei mit allen FEM-Informationen zum Export nach ANSYS vorzubereiten.
Dadurch werden die FEM-relevanten Daten in einer Datei gespeichert, die von ANSYS gelesen werden kann.
- Geben Sie den Namen der Datei, die die in ANSYS zu exportierenden FEM-Informationen enthält, in das Textfeld ein.
- Sie können auch auf Speichern unter klicken, um eine bestehende Datei auszuwählen oder eine Datei zu erstellen.
Wenn Sie eine bestehende Datei auswählen, überschreibt die Software alle in der Datei enthaltenen Daten.
Anmerkung: Wenn Sie Ansys Workbench 10 oder 11 verwenden, nehmen Sie eine zusätzliche Änderung der Datei vor. Öffnen Sie die Textdatei, und suchen Sie den Abschnitt mit der Überschritt "Inertial State". In diesem Abschnitt befinden sich zwei Zeilen, die entfernt werden müssen. Dabei handelt es sich um die Zeilen "Grounded" und den zugewiesenen Code ("0" oder "1") in der darauffolgenden Zeile.
- Klicken Sie auf
Weitere Optionen, um zusätzliche Eigenschaften anzuzeigen.
- Wenn Sie Urheberrechtsinformationen für die von Ihnen erstellten AVI-Dateien anzeigen möchten, klicken Sie auf Copyright auf AVIs anzeigen, und geben Sie die entsprechenden Urheberrechtsinformationen in das Textfeld ein.
- Klicken Sie auf Winkelgeschwindigkeit in Umdrehungen pro Minute eingeben (rpm), um Winkelgeschwindigkeiten in Umdrehungen pro Minute einzugeben.
Die Ausgabe erfolgt jedoch in den Einheiten, die Sie bei Auswahl der leeren Baugruppendatei festgelegt haben.
- Um die Länge der Z-Achse des Baugruppenkoordinatensystems für 3D-Rahmen im Grafikfenster festzulegen, geben Sie den Prozentwert in das Feld Größe von Z-Achse ein.
Die Z-Achse entspricht vorgabegemäß 20 % der Diagonalen des virtuellen Rahmens.
- Klicken Sie auf OK oder auf Anwenden.
In beiden Fällen werden die Einstellungen gespeichert. Bei Auswahl von OK wird zudem das Dialogfeld geschlossen.
Mikromechanismusmodell
Diese Option dient zur Arbeit mit Mechanismen, die kleine Masseeigenschaften haben.
Im Standardmodus schlägt die Berechnung fehl, falls die Masse oder Trägheit kleiner als 1e-10 kg oder 1e-16 kg/m2 ist. Die dynamische Gleichung wird dann mit einem Gauß-Verfahren mit einer Präzision von 1e-10 gelöst (unter diesem Wert ist der Drehpunkt auf 0 gesetzt).
Wenn der Mikromechanismusmodus aktiviert ist, muss die Masse oder Trägheit größer als 1e-20 kg und 1e-32 kg/m2 sein. Die Gauß-Präzision wird auf 1e-32 eingestellt.
Um zu bestimmen, wann diese Option aktiviert werden sollte, prüfen Sie die Masseeigenschaften im Gelenkkoordinatensystem.
- Falls ein Übersetzungsfreiheitsgrad vorliegt, wird die Masse geprüft.
- Falls ein Rotationsfreiheitsgrad entlang der X-Achse vorliegt, wird die Hauptträgheit Ixx entlang der X-Achse geprüft, nicht die Querträgheiten Ixz und Ixy, die hier nicht von Interesse sind.
|
Beispiel 1 |
|
| Sie haben einen Mechanismus, in dem das kleinste Bauteil die Masse m = 6,5e-9 kg hat und die Hauptträgheiten Ixx = 1e-20 kg/m2, Iyy = 1e-20 kg/m2 betragen, selbst wenn Izz > Trägheitsgrenze = 1e-10 kg/m2: | |
|
|
Assembly Precision (Baugruppengenauigkeit)
Nur für geschlossene Konturen und 2D-Kontakte gültig.
2D-Kontakt: Definiert den maximal zulässigen Abstand zwischen Kontaktpunkten. Der Standardwert lautet 1e-6m = 1μm.
- Der Abstand wird immer zum Abschluss der Runge-Kutta-Schritte überprüft.
- Wenn der Abstand zwischen diesen Punkten nicht die Baugruppengenauigkeit überschreitet, werden die Positionen und Geschwindigkeiten angenommen, und die Berechnung wird mit dem Schätzwert für Integrationsfehler fortgesetzt.
- Wenn der Abstand die Baugruppengenauigkeit überschreitet, werden die Positionen korrigiert, bis der Abstand die Baugruppengenauigkeit nicht mehr überschreitet. Basierend auf diesen neuen Positionen werden die Geschwindigkeiten angepasst, und die Berechnung wird mit dem Schätzwert für Integrationsfehler fortgesetzt.
Geschlossene Kontur: Wie 2D-Kontakt; sie kann jedoch je nach Gelenktyp Winkelabhängigkeiten haben (angegeben im Bogenmaß rad).
- Abstand und Winkelabhängigkeiten werden zum Abschluss der Runge-Kutta-Schritte überprüft.
- Wenn die Abstandsabhängigkeiten nicht die Baugruppengenauigkeit überschreiten und die Winkelabhängigkeiten nicht die Baugruppengenauigkeit multipliziert mit 1e3 überschreiten (Baugruppengenauigkeit angegeben in Metern), werden die Position und Geschwindigkeiten angenommen, und die Berechnung wird mit dem Schätzwert für Integrationsfehler fortgesetzt.
- Anderenfalls werden die Positionen so lange korrigiert, bis die Abstandsabhängigkeiten nicht mehr die Baugruppengenauigkeit überschreiten und die Winkelabhängigkeiten nicht mehr die Baugruppengenauigkeit multipliziert mit 1e3 überschreiten. Die Geschwindigkeiten werden dann korrigiert, und die Berechnung wird mit dem Schätzwert für Integrationsfehler fortgesetzt.
Ändern der Baugruppengenauigkeit
Der Parameter Assembly Precision (Baugruppengenauigkeit) kann in den folgenden Situationen geändert werden:
- Der Mechanismus kann nicht zu Beginn oder während der Simulation zusammengebaut werden. Überprüfen Sie zuerst die Umsetzbarkeit des Mechanismus: Ist die angeforderte Position realistisch und kann sie vom Mechanismus erreicht werden. Überprüfen Sie angewendete Bewegungen, die zu gegensätzlichen Positionen führen können. Wenn kein Problem erkannt wird und der Maßstab des Mechanismus groß ist (Größe von 1 m), erhöhen Sie die Baugruppengenauigkeit (1e-5m oder 1e-4m). Wenn der Maßstab klein ist (kleiner als 10 mm), reduzieren Sie die Baugruppengenauigkeit (1e-7m oder 1e-8m).
- Wenn der Mechanismus kleiner als 1 mm ist, reduzieren Sie die Baugruppengenauigkeit (1e-8m bis 1e-10m), oder verwenden Sie das Mikromechanismusmodell.
Solver Precision (Lösergenauigkeit)
Dynamische Gleichungen werden mit einem fünfstufigen Runge-Kutta-Integrationsschema integriert. Der Integrationsfehler und Zeitschritt werden folgendermaßen verwaltet, um eine Annahme sicherzustellen:
- Am Ende jedes Runge-Kutta-Schritts wird der Integrationsfehler anhand der berechneten Geschwindigkeiten und Beschleunigungen geschätzt.
- Dieser Integrationsfehler wird mit dem benutzerdefinierten Parameter "Solver Precision" (Lösergenauigkeit) verglichen.
- Wenn der Integrationsfehler nicht die Lösergenauigkeit überschreitet, wird der Schritt akzeptiert, und die Integration wird fortgesetzt.
- Wenn der Integrationsfehler die Lösergenauigkeit überschreitet, wird der Schritt abgelehnt. Dann wird ein neuer Zeitschritt, kleiner als der tatsächliche Zeitschritt, berechnet, und die Simulation wird am Anfang des Schritts mit dem neuen Wert für den Zeitschritt neu gestartet.
Der Integrationsfehler wird unter Verwendung bestimmter Eigenschaften der Runge-Kutta-Formeln geschätzt. Dies ermöglicht eine einfache Berechnung der Positionen "p" und Geschwindigkeiten "v" bis zur fünften Ordnung (Vektoren "p5" und "v5") und zur vierten Ordnung (Vektoren "p4" und "v4"). Der Integrationsfehler wird dann wie folgt anhand von Positionen und Geschwindigkeiten definiert:
|
Integ_fehler_position = norm(p5 - p4) Integ_fehler_geschw = norm(v5 - v4) Dabei steht "norm" für eine Spezialnorm. |
Wenn ein Schritt akzeptiert wurde, ist folgende Beziehung vorhanden (in metrischen Einheiten):
|
Integ_fehler_position = norm(p5 - p4) < Atol + | p5 | . Rtol Integ_fehler_geschw = norm(v5 - v4) < Atol + | v5 | . Rtol |
Mit:
| Atol | Rtol | |
|---|---|---|
|
Übersetzungsfreiheitsgrad |
Solver Precision (Lösergenauigkeit) Standard = 1e-6 Kein Maximalwert |
Solver Precision (Lösergenauigkeit) Standard = 1e-6 Kein Maximalwert |
|
Drehfreiheitsgrad |
Solver Precision (Lösergenauigkeit) . 1e3 Standard = 1e-3 Maximalwert = 1e-2 |
Solver Precision (Lösergenauigkeit) . 1e3 Standard = 1e-3 Maximalwert = 1e-2 |
Um diesen Prozess zu veranschaulichen, betrachten Sie folgendes Beispiel:
|
Beispiel 1: Relativer Fehler Rtol |
|
|
Gelenktyp: Gleitgelenk 1 mit Position und Geschwindigkeit |
|
|
p[1] = 4529.289768 m v[1] = 18.45687455 m/s |
|
|
Falls Solver Precision (Lösergenauigkeit) auf 1e-6 eingestellt ist (der Standard), sind Ergebnisse mit sechs Ziffern garantiert: |
|
|
p[1] = 4529.28 m v[1] = 18.4568 m/s |
|
|
Falls Solver Precision (Lösergenauigkeit) auf 1e-8 eingestellt ist, sind acht Ziffern garantiert: |
|
|
p[1] = 4529.2897 m v[1] = 18.456874 m/s |
|
|
Beispiel 2: Relativer Fehler für Atol |
|
|
Gelenktyp: Gleitgelenk 1 mit Position und Geschwindigkeit |
|
|
p[1] = 0.000024557 m v[1] = 0.005896476 m/s |
|
|
Falls Solver Precision (Lösergenauigkeit) auf 1e-6 eingestellt ist (der Standard), sind Ergebnisse mit sechs Nachkommastellen garantiert: |
|
|
p[1] = 0.000024 m v[1] = 0.005896 m/s |
|
|
Falls Solver Precision (Lösergenauigkeit) auf 1e-8 eingestellt ist, sind acht Nachkommastellen garantiert: |
|
|
p[1] = 0.00002455 m v[1] = 0.00589647 m/s |
|
| Dasselbe gilt für eine Stiftverbindung, jedoch haben Atol und Rtol gleiche Lösergenauigkeit, multipliziert mit 1e3: | |
|
Beispiel 3: Relativer Fehler für Rtol |
|
|
Gelenktyp: Stiftverbindung 2 mit Position und Geschwindigkeit |
|
|
p[2] = 12.53214221 rad v[2] = 21.36589547 rad/s |
|
|
Falls Solver Precision (Lösergenauigkeit) auf 1e-6 eingestellt ist (der Standard), sind Ergebnisse mit drei Ziffern garantiert: |
|
|
p[2] = 12.5 rad v[2] = 21.3 rad/s |
|
|
Falls Solver Precision (Lösergenauigkeit) auf 1e-8 eingestellt ist, sind fünf Ziffern garantiert: |
|
|
p[2] = 12.532 rad v[2] = 21.365 rad/s |
|
Der Parameter Solver Precision (Lösergenauigkeit) kann in den folgenden Situationen geändert werden:
- Die Simulation wird mit einer Fehlermeldung angehalten und der Zeitschritt ist klein genug, um ein qualitativ hochwertiges Ergebnis zu erzielen. Wenn kleine Verschiebungen auftreten, verringern Sie die Lösergenauigkeit. Wenn große Verschiebungen auftreten, vergrößern Sie die Lösergenauigkeit.
- Bei aktivierten 2D-Kontakten (Status = 1). Wenn kleine Kräfte auftreten, verringern Sie die Lösergenauigkeit. Wenn große Kräfte auftreten, vergrößern Sie die Lösergenauigkeit. Dies gilt nicht für Kräfte bei Schockeinwirkungen.
- Bei der Arbeit mit kleinen Mechanismen (weniger als 1 mm). Verringern Sie in diesen Fällen die Lösergenauigkeit, oder aktivieren Sie die Option Mikromechanismusmodell.
Capture Velocity (Erstellgeschwindigkeit)
Dieser Parameter wird für die Simulation von Zusammenstößen zwischen Objekten verwendet. Er hilft dem Löser dabei, die Anzahl der kleinen Stöße zu beschränken, bevor konstante Kontakte auftreten. Das Stoßmodell verwendet einen Rückstoßkoeffizienten (d. h. eine Stoßzahl) "e". Der vom Benutzer eingegebene Wert liegt zwischen 0 und 1. Für die sich daraus ergebenden Bedingungen werden die Werte wie folgt behandelt:
- Wenn e = 0: maximaler Energieverlust. Beispiel: Nehmen Sie einen einfachen Ball, der von einer Anfangshöhe ohne Anfangsgeschwindigkeit auf eine Ebene fällt – unter der Auswirkung der Schwerkraft prallt er nicht sichtbar ab.
- Wenn e = 1: kein Energieverlust. Wir bleiben beim Beispiel des Balles: Der Ball prallt ab und kehrt an seine Ausgangsposition zurück, der Kontaktstatus = 0.5. Die Bewegung erfolgt periodisch und wird unbegrenzt fortgesetzt.
- Wenn e>0 und e<1: Energieverlust bei jedem Aufprall. Wieder das Ballbeispiel: Der Ball prallt ab, aber die Sprunghöhe verringert sich nach jedem Aufprall. Nach Erreichen der Grenze bleibt der Ball auf der Ebene liegen, zu diesem Zeitpunkt ist der Kontaktstatus = 1. Unter diesen Bedingungen ist die Erstellgeschwindigkeit wirksam.
Der Parameter Capture Velocity (Erstellgeschwindigkeit) hilft dem Löser dabei, die Anzahl der kleinen Stöße zu beschränken, bevor der Kontakte als aktiv oder konstant angesehen wird. Der Erstellvorgang läuft wie folgt ab:
- Zur Berechnung des Aufpralls werden alle Rückgabekoeffizienten auf ihre Anfangswerte zurückgesetzt.
- Relative Geschwindigkeiten nach dem Aufprall, die Abhebegeschwindigkeiten darstellen, werden für alle Kontakte mit dem Erstellgeschwindigkeits-Parameter verglichen.
- Falls alle relativen Geschwindigkeiten größer als die Erstellgeschwindigkeit oder als Null sind, wird der Aufprall akzeptiert und der Löser schreitet mit den neuen Geschwindigkeiten als Anfangsparameter in der Zeit fort.
- Falls eine relative Geschwindigkeit kleiner als die Erstellgeschwindigkeit, aber ungleich Null ist, wird e = 0 für diesen Kontakt angenommen, um den Energieverlust zu maximieren, und der Aufprall wird erneut berechnet. Wenn der Aufprall übernommen wird, werden alle Rückgabekoeffizienten auf ihre Anfangswerte zurückgesetzt.
Wann kann der Parameter geändert werden?
Der Parameter kann in den folgenden Situationen geändert werden:
- Wenn Sie 2D-Kontakte haben und die Simulation langsam ist. Stoppen Sie die Simulation, plotten Sie die Erstellgeschwindigkeit. Wenn der Parameter bei jedem Zeitschritt variiert (zwischen 0 - 1 - 2) oder gleich 1 ist, gibt es ein Problem. Der Löser versucht, den Status der Kontakte zu stabilisieren, aber dies braucht Zeit und ist komplex. Erhöhen Sie in diesem Fall die Erstellgeschwindigkeit.
- Es entstehen keine Vorteile durch die Reduzierung des Parameterwertes.
Regularization Velocity (Regulierungsgeschwindigkeit)
Bei 2D-Kontakten wird ein reales nicht-lineares Coulombsches Reibungsgesetz angewendet. Für Verbindungen und 3D-Kontakte wird ein standardisiertes Coulombsches Gesetz angewendet, zur Vereinfachung und um eine hyperstatische Bedingung zu vermeiden. Dieses kann wie folgt veranschaulicht werden:
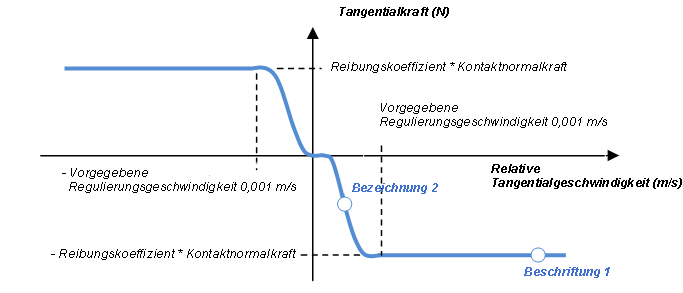
Die Regulierung wird durch den Parameter Regularization Velocity (Regulierungsgeschwindigkeit) gesteuert.
Wenn Sie dieses Modell für Haftkontakte (oder Rollkontakte) verwenden und die relative Tangentialgeschwindigkeit Null beträgt, ist die Tangentialkraft Null.
Im Falle von Gelenkreibung in einem Drehfreiheitsgrad wird die tangentiale Kraft durch einen tangentialen Drehmoment (Einheit: Nm) ersetzt, und die tangentiale relative Geschwindigkeit ist eine Drehgeschwindigkeit (Einheit: rad/s). Beide werden durch Multiplikation der tangentialen Kraft mit dem und Division der Übersetzungsgeschwindigkeit durch den Gelenkradius berechnet.
|
Beispiel 1 |
|
|
Eine Stiftverbindung mit einem Radius von 10 mm wird mit der konstanten Geschwindigkeit "w" gleich 10 rad/s gesteuert. Es wird eine Kraft (Fn) von 20 N lotrecht zur Drehachse auf die Verbindung angewendet, und der Reibungskoeffizient (mu) ist auf 0.1 eingestellt. In diesem Fall kann das Reibungsdrehmoment (Uf) im Gelenk wie folgt berechnet werden: |
|
|
? = r * w = 0.01 * 10 = 0.1 m/s ? > Regulierungsgeschwindigkeit = 0.001 m/s => Uf = -mu * r * Fn = -0.1 * 0.01 * 20 = -0.02 Nm Siehe "Tag 1" im standardisierten Coulombschen Diagramm. |
|
|
Beispiel 2 |
|
|
Dasselbe Beispiel mit einer Geschwindigkeit (w) von 0.05 rad/s ergibt ein Reibungsdrehmoment (Uf) von: |
|
|
? = r * w = 0.01 * 0.05 = 0.0005 m/sm ? > Regulierungsgeschwindigkeit = 0.001 m/s => Uf ≈ -mu * r * Fn/2 = -0.1 * 0.01 * 20/2 = -0.01 Nm Siehe "Tag 2" im standardisierten Coulombschen Diagramm. |
|
Der Parameter Regularization Velocity (Regulierungsgeschwindigkeit) kann in den folgenden Situationen geändert werden:
- Die Simulation ist langsam, und es treten kleine Oszillationen an einem Gelenk mit Reibung oder an einer 3D-Kontaktverbindung auf. Die Reibung im Gelenk oder am 3D-Kontakt erzeugt eine bezeichnende Steifigkeit im Modell, deshalb verringert der Löser den Zeitschritt, um eine zuverlässige Präzision zu gewährleisten. Sie müssen die Steifigkeit verringern => erhöhen Sie den Parameter Regularization Velocity (Regulierungsgeschwindigkeit) um den Faktor 5 (5e-3 m/s). Falls das Modell weiterhin langsam ist, können Sie den Parameter weiter mit Werten, die relativ zum Modell sind, erhöhen (niedriger im Vergleich zu den Geschwindigkeiten im Modell).
- Die Regulierungsgeschwindigkeit sollten Sie nicht deutlich erhöhen, sonst funktioniert sie nur zwischen diesen Werten. Die Reibungskraft erreicht niemals ihren Maximalwert. Daher wird der Reibungseffekt künstlich eingeschränkt.
Numerische Prüfung
Bevor Sie die Simulationsergebnisse analysieren, sollten Sie prüfen, ob die Simulation numerisch gültig ist, also nicht von numerischen Parametern beeinflusst wird. Um die numerische Prüfung durchzuführen, gehen Sie wie folgt vor:
- Führen Sie eine Simulation mit einem Satz numerischer Parameter (Löser- und Baugruppengenauigkeit, Erstellgeschwindigkeit, Regulierungsgeschwindigkeit und Zeitschritt), und speichern Sie sie.
- Teilen Sie jeden Parameter durch 10, führen Sie die Simulation aus, und speichern Sie sie.
- Plotten Sie alle Ergebnisse im selben Diagramm. Falls alle Ihre Ergebnisse ähnlich sind, wird die Simulation nicht von numerischen Parametern beeinflusst. Andernfalls gibt es ein Empfindlichkeitsproblem.
- Wenn die Simulation nicht beeinflusst wurde, können die Ergebnisse analysiert werden.
- Wird die Simulation jedoch von numerischen Parametern beeinflusst, bestimmen Sie anhand der Ergebniskurven, welcher numerische Parameter den Einfluss ausübt. Teilen Sie den Parameter durch 10, und verwenden Sie das Ergebnis als Nennwert für den numerischen Parameter. Starten Sie die Prüfung erneut. Um Zeit zu sparen, können Sie die Unbeeinflussbarkeit für den einen Parameter testen.