Coons' Method

Coons' surfaces are 3D surfaces spread over quadrilateral or triangular contours whose opposite sides are divided into the same number of segments. The shapes of the created elements correspond to the region on which the mesh is created. Using this method, all points created on the selected contour edge are connected with the points on the opposite edge of the contour. The cutting point of each pair of horizontal and vertical lines marks the end positioning of the node inside the region, as shown.

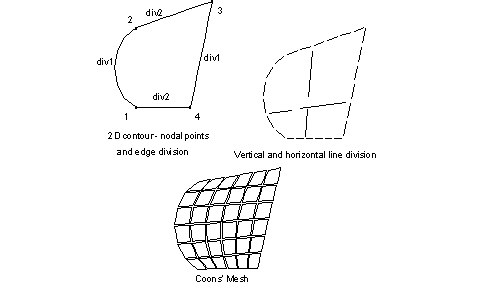
After you select the contour, you define the parameters of Coons' method, which describe the FE mesh shape (triangles, quadrilaterals, mixed element type) as well as the division parameters. The division parameters describe the number of the elements that will be created on the first contour edge (between the first and the second contour corner) and the second contour edge (between the second and third contour corner). The contour edges opposite the listed contour edges will be automatically divided, so that the division corresponds to the division accepted on the first and second contour edges. For triangular regions, the edge division between the third and first contour corners is the same as that between the second and third corners. In quadrilateral regions, the division between the third and fourth contour corners is the same as between the second and third corners. If 2 divisions are different (for example, if the division between the third and fourth contour corners is larger than the division between the first and second corners due to a user-defined value), the edge contour division with the manual value will be automatically increased.

You can apply Coons' meshing to flat (2D) domains where contours are defined on planes (see drawing above) as well as for 3D surfaces where contours are defined in space (see drawing below).

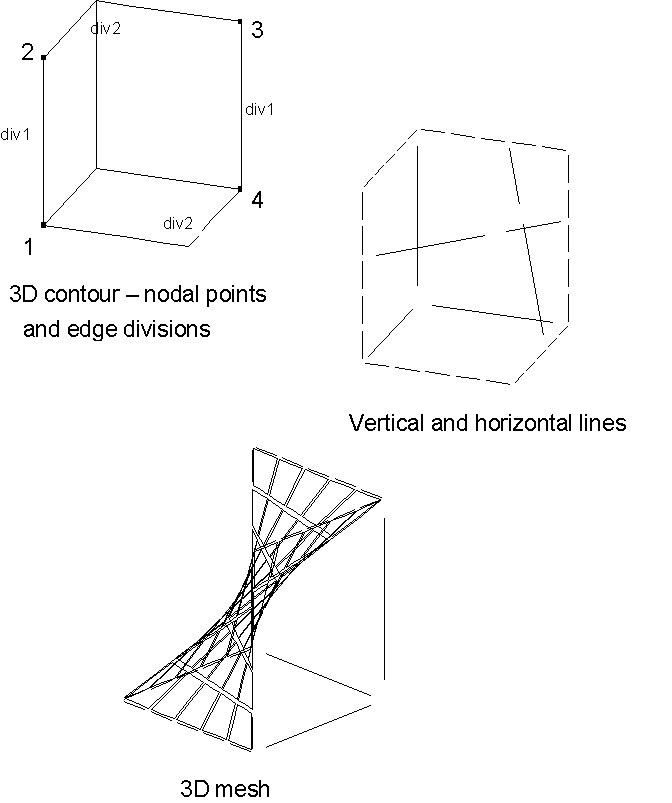
Parameters that may be defined for Coons' method:

FE mesh type (Coons' typology)
Mesh creation parameters (division1 and division2)