Single-Span is Inherently Smooth
A single span curve or surface is always smooth, whereas multi-span can have a continuity break between the spans.
This can be seen by applying a curvature comb using Evaluate > Curve Curvature.
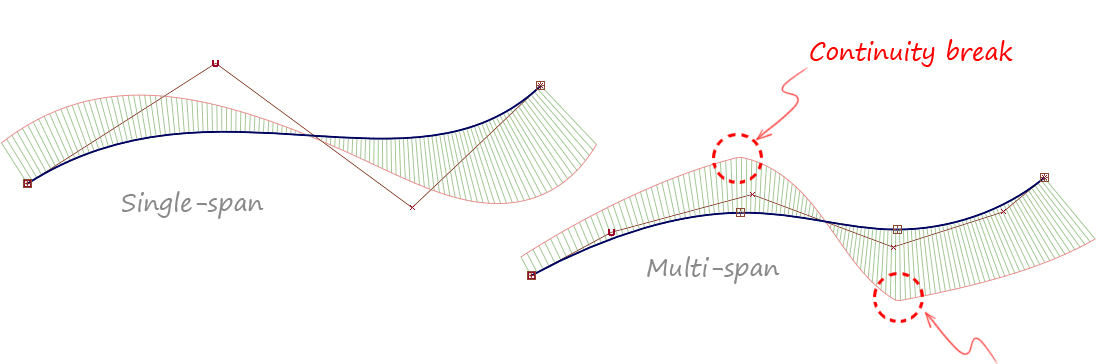
A 'continuity break' is any deviation from a smooth curvature comb plot. To be more precise, you need to understand what continuity level you are aiming for. More technical information on this can be found in the Evaluation 1: Curve Curvature Theory Builder.
In practice, we use our visual judgement to notice a 'smooth' or 'lumpy' curvature plot.
Applying the Rule
Most experienced users get into the habit of starting with single-span curves by placing the start and end Edit Points:
- Use Curves > New Curves > New Edit Point Curve
- Click in two positions, once for the start and once for the end of the curve
- Pick and move CVs to the desired shape
- Modify the Degree to change the number of CVs if you need more controls

If you prefer to use the CV creation method, you can use the Progressive Degree setting which automatically increases the Degree instead of the Spans as you place additional CV positions. Setting the maximum Curve Degree to 7 allows up to 8 CVs.

Breaking the Rule
Some of the most useful surface tools, like Freeform Blend or Surface Fillet will often produce multi-span surfaces. During concept and development work, these are usually good enough for design iterations.
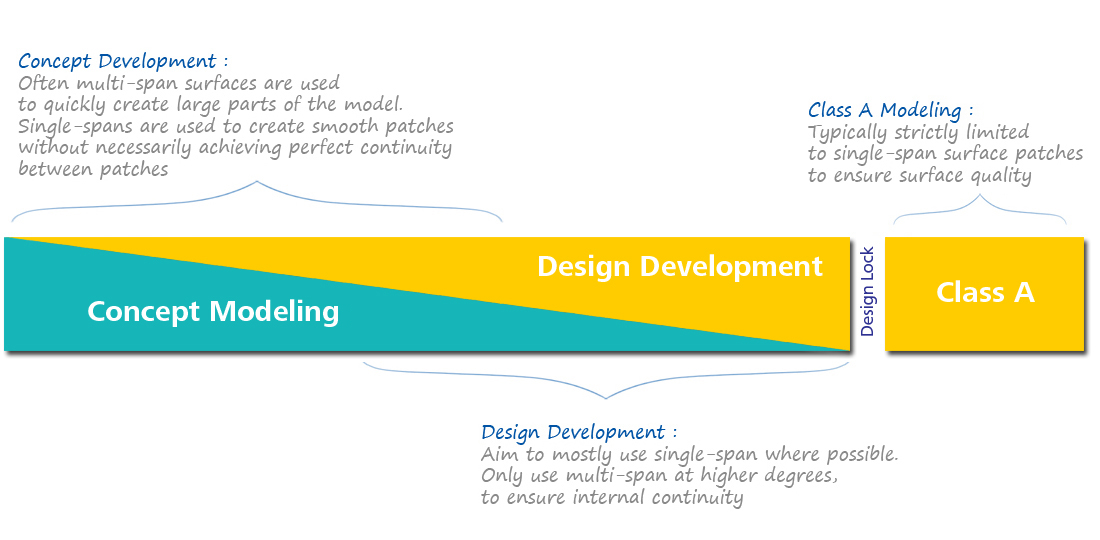
Theory and Practice
A more technical way of discussing 'smooth' is to talk about 'continuity'. We work with continuity in two ways:
- Continuity between two surfaces or curves.
- Internal Continuity within a single surface or curve.
It is Internal Continuity that is considered here – how smooth a curve is within itself.
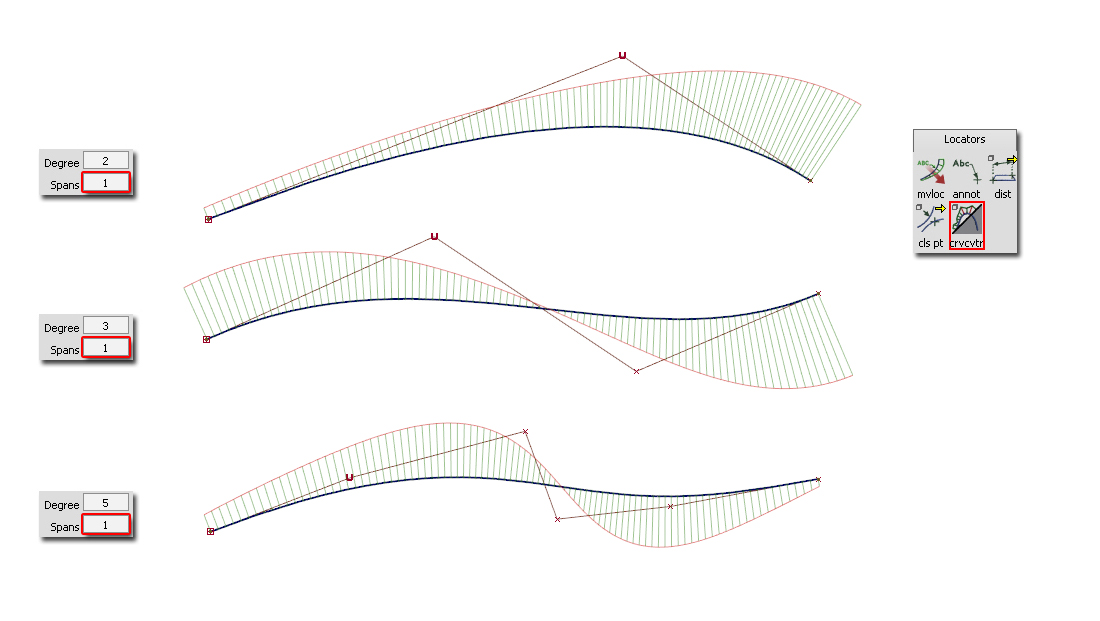
Continuity & Degree on Single-Span (Bezier)
A single-span curve or surface will always remain smooth and continuous, regardless of the Degree:
Continuity & Degree on Multi-Span
Continuity breaks can occur between spans, but the effect is reduced with higher Degree. The following examples are all 3-Span curves, but with different Degree:
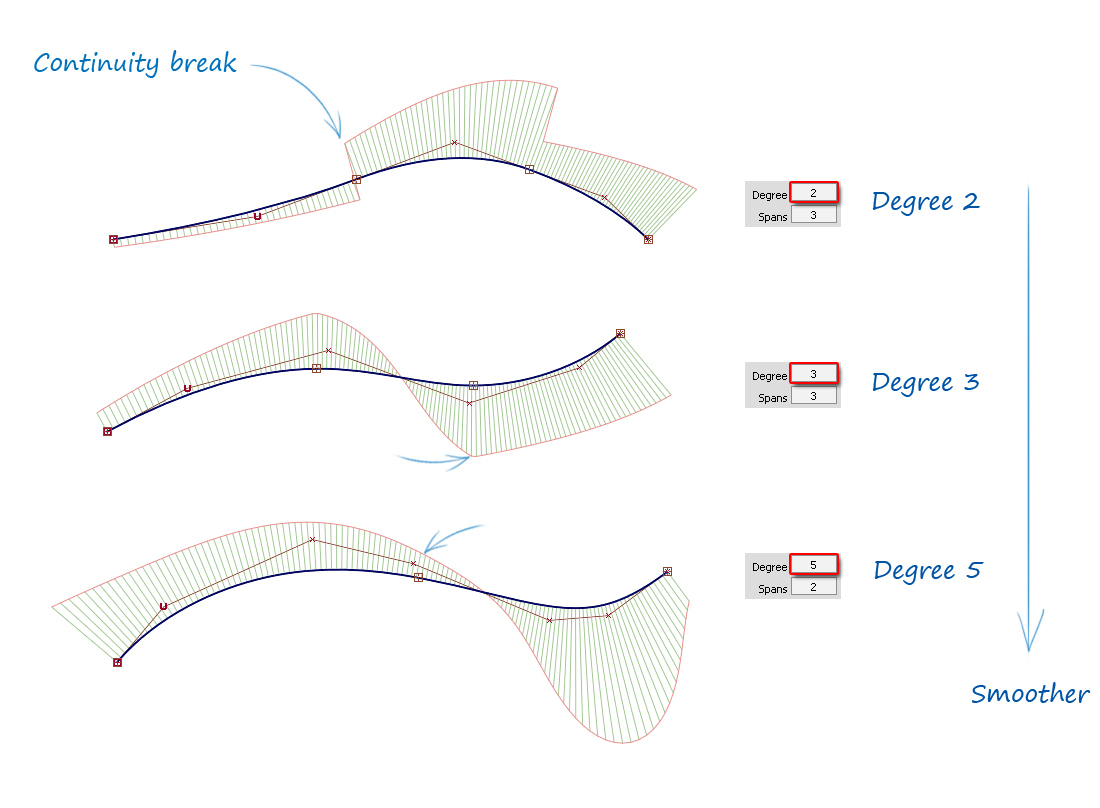
The internal continuity between spans is directly related to the Degree (shown below). So if you need to use multi-span curves or surfaces, choosing higher Degrees will make the result more smooth.
| Degree | Internal Continuity |
|
1 |
G0 |
|
2 |
G1 |
|
3 |
G2 |
|
4 |
G3 |
|
5 |
G4 |
|
6 |
G5 |
|
7 |
G6 |
A good example is a Curve > Circle with different Degrees:
