A modal or natural frequency analysis (also known as normal modes or eigenvalue analysis) forms the basis of several other dynamic analyses, including the modal approach formulations and response spectrum analysis. In addition, the results of a modal analysis will tell you much about the dynamic characteristics of the model, including whether or not you really have a dynamic system at all. For this reason, analysts often run a normal modes analysis first to examine the basic model dynamics and to check for modeling problems.
The results of this analysis produces a mode shape and frequency. Note that the output mode shape is an eigenvector with the maximum value set to 1.0. Thus, the resulting deformations are scaled such that the largest deformation within the structure is 1.0 and is not representative of the scale of the deformations expected during actual vibrations.
Modal analysis can include constraints or not. Models run without constraints should have their first 6 vibration frequencies of essentially 0 since it's a "free" mode. Partially constrained models will have less than 6 "free" modes.
Eigenvalue Theory
Consider a dynamic system. In general, the equations of motion can be expressed as a function of the system mass, stiffness, damping and applied loads:
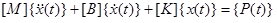
where:
[M] = global mass matrix
[K] = global stiffness matrix
[B] = global damping matrix
{P} = global load vector
Eigenvalues or natural frequencies are found when there is no damping or applied loads. The equations of motion for free vibration can then be written as:
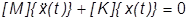
Assume a sinusoidal vibration, where the displacement can be described by:
Then replace the {x(t)} term with the above and consider that, for a sinusoidal variation, the acceleration is the second derivative of the displacement:
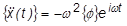
Thus the equation of motion becomes:
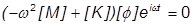
Since
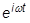is never zero, the equation can be rearranged to the form of a general eigenvalue problem.
Inventor Nastran determines the natural frequency by solving the eigenvalue problem:
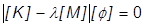
where:
[K] = global linear stiffness matrix
[M] = global mass matrix
= the eigenvalue for each mode that yields the natural frequency =
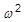
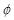= the eigenvector for each mode that represents the natural mode shape
The eigenvalue is related to the system’s natural frequency:
where:
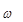= the circular frequency (radians per second)
or in Hertz:
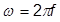
where:
f = the cyclic frequency (Hertz)
One solution is trivial (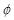 = 0), but the other solutions for
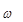are interesting.
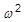is called the eigenvalue
, and each is accompanied by a unique
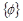called the eigenvector.
In solving the above eigenvalue problem, there are as many eigenvalues and corresponding eigenvectors as there are unconstrained degrees of freedom. Often, however, only the lowest natural frequency is of practical interest. This frequency will always be the first mode extracted.
The solution of the eigenvalue problem is difficult and a number of different approaches have been developed over the years. Currently the Lanczos approach is favored as it is fast, accurate and robust. Inventor Nastran also offers the Subspace method. This can be used in those rare cases where Lanczos fails. SUBSPACE is selected using the Nastran directive EXTRACTMETHOD=SUBSPACE in the Parameters dialog box under Program Control Directives (select the Advanced Settings checkbox first). For more details, see the Parameters topic of the User's Guide. The default AUTO setting for this parameter uses Lanczos in most circumstances, but changes to Subspace for some small problems. Note that Inventor Nastran does not recognize the EIGR card available in other Nastrans to use other extraction methods.
Also, while the
found is the exact eigenvalue, the eigenvectors are arbitrarily scaled. That is, there is no unique magnitude to the vectors. They simply represent a shape. By default,
Inventor Nastran performs a mass scaling on the vectors. This is done by calculating the generalized mass of the model from the equation:
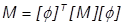
All of the terms of the vector are then divided by it. This results in a seemingly arbitrary scaling of the vectors, but it has important mathematical properties that can be exploited elsewhere. In addition to mass scaling, Nastran also has max scaling available, where the largest value in the vector will be 1.0. This allows small vectors to be examined manually.
A property of eigenvectors is that they are orthogonal. This means that one eigenvector multiplied by another will produce an identity matrix. An eigenvector vector multiplied by itself will be zero.
This is another property that is exploited in dynamics solutions.
Rigid Body Modes
Modal analyses are usually divided into two types based on the constraints:
- If the model is unconstrained (such as a rocket or aircraft in flight), it is referred to as a free-free analysis, after the corresponding beam representation, i.e. a beam analyzed this way would be free at both ends. When a modal analysis is run on a free-free system, there will be six zero-frequency rigid body modes (or mechanism modes) found in addition to the elastic modes. These modes represent the free translation and rotation of the system in the six directions of motion and will be extracted as modes one through six. Mode seven is then refereed to as the first flexible mode and will not be a zero energy mode. It is always a good model check to run an unconstrained modal analysis to assure that you are finding these modes. This way, you'll know that the model is not internally constrained accidentally. Some systems really are unconstrained, and unlike a static analysis, a modal analysis can be run successfully on a free-free structure.
- The other type of modal analysis is a constrained system. In this case, there should be no zero-frequency modes. If any are found, it is an indication that some portion of the model is free to move in a rigid body manner. This type of motion is usually referred to as a mechanism. And while a modal analysis can solve this type of problem, a static analysis will fail. For this reason, a modal analysis is often used as a debugging tool for a static analysis that has failed. Once the source of the zero frequency mode is identified, it can be constrained and a static analysis successfully run.
Mechanism modes occur in an insufficiently constrained structure where a portion of the structure displaces as a rigid body. An example would be a flat plate on a hinge or a ball joint. A mechanism mode can also occur when two parts of a structure are not connected properly. A common example of this is a bar connected to a solid element.
Rigid body and mechanism modes are indicated by zero or near-zero frequency eigenvalues. For most structures, near-zero should be on the order of 1.0E-3 Hz or less and may be negative.
|
Previous Topic: Dynamic Analysis |
Next Topic: Modal Analysis Exercise |