A fillet arc is an arc created between two objects such that the tangents of the arc lie on each object.
You can also create fillet arcs on composite curves where two lines meet.
To create a fillet arc between two objects:
- Create two objects you wish to create the fillet arc between.
The two objects can be one of the following:
- two lines
- two arcs
- one arc and one line.
Suppose we have the following lines.

- Click Wireframe tab > Create panel > Fillet > Fillet Arc for a trimmed fillet arc, or Fillet Arc Untrimmed for an untrimmed fillet arc.
The Fillet Arc option trims the original lines to leave only the new fillet. The Fillet Arc Untrimmed option leaves the original lines intact.
Notice that the mouse cursor has changed to an arc with a value attached and an arrow. The attached value is the default radius value:
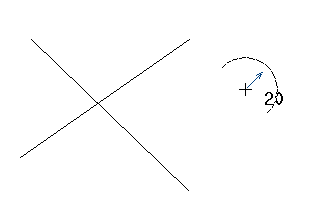
To change the default radius during the fillet arc creation, type the radius command r directly in the graphics window, followed by the new value. For example:
r 50
Press Enter.
The new radius value becomes the default radius value and is now attached to the cursor. You can also change the default radius value using the Arcs page of the Options dialog.
If you move the cursor over a suitable object, the intelligent cursor tells you that you can select this object as the first item:
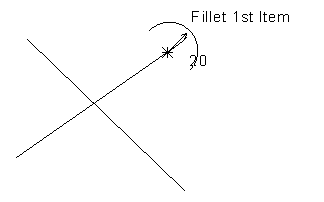
- Select one object and then the other.
For two lines which cross, there are four fillet arc solutions as shown below. Therefore, where you select the lines is important.
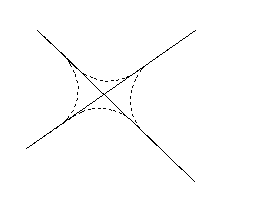
Make sure you select the lines on the same side of the intersection where you want the fillet arc to lie.
Suppose we want the following Fillet Arc (trimmed):

We can select the two lines anywhere as shown below:
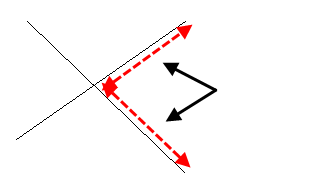
Fillet arcs are added to composite curves where two lines meet. These fillet arcs become part of the composite curve.
To create a fillet arc on composite curves:
- Create a composite curve, for example:
- Click Wireframe tab > Create panel > Fillet > Fillet Arc for a trimmed fillet arc, or Fillet Arc Untrimmed for an untrimmed fillet arc.
The cursor has changed to an arc with a value attached and an arrow. The attached value is the default radius value. Change the default radius type as described above.
When you hold the cursor over the composite curve, the intelligent cursor shows where the new fillet arcs will lie (see figure below):
Note: In the figure below, 20 is the default radius value and 7.5 is the gridding distance from the nearest key point on the composite curve.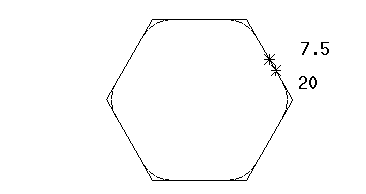
- Select the composite curve.
If two lines meet anywhere in the composite curve, a fillet arc is added.
In our example, six fillet arcs are added to our composite curve:
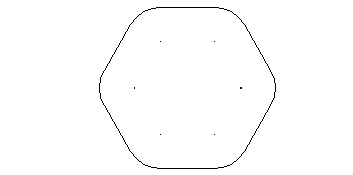
The fillet arcs are edited as part of the composite curve.