El generador de cadenas de rodillo recurre a la siguiente teoría para informar a los usuarios de si la cadena seleccionada funciona correctamente en las condiciones de funcionamiento especificadas.
El factor estático de seguridad de ruptura de la cadena se calcula para cargas constantes mediante la siguiente fórmula:
![]()
donde:
|
S Smin |
Coeficiente de seguridad estática mínimo admitido [-] |
|
|
F U |
Resistencia máxima a tracción de la cadena [N] |
|
|
F Tmax |
Tensión máxima en el intervalo de la cadena especificado [N] |
El factor dinámico de seguridad de ruptura de la cadena se calcula para picos de cargas mediante la siguiente fórmula:
![]()
donde:
|
S Dmin |
Coeficiente de seguridad dinámica mínimo admitido [-] |
|
|
F U |
Resistencia máxima a tracción de la cadena [N] |
|
|
F Tmax |
Tensión máxima en el intervalo de la cadena especificado [N] |
|
|
Y |
Factor de impacto [-] |
Potencia de diseño y potencia de cadena
La potencia de cadena P R está relacionada con la potencia de diseño P D . La potencia de cadena debe ser más grande que la potencia de diseño.
P D < P R
donde:
|
|
||
|
|
||
|
P |
potencia para transmitir [W] |
|
|
P RN |
Potencia de cadena de un único tramo en condiciones normales de funcionamiento [W] |
|
|
f 1 |
Factor de servicio [-] |
|
|
f 2 |
Factor de tamaño de rueda dentada [-] |
|
|
f 3 |
Factor de tramos de cadena [-] |
|
|
f 4 |
Factor de lubricación [-] |
|
|
f 5 |
Factor de distancia entre ejes/centros [-] |
|
|
f 6 |
Factor de coeficiente [-] |
|
|
f 7 |
Factor de vida útil [-] |
|
| Φ |
Factor de construcción de cadena [-] |
|
La potencia de cadena se calcula mediante ecuaciones empíricas de potencia exclusivas para cada cadena. Estas ecuaciones se mencionan en las normas nacionales de cadenas de acero y se pueden obtener también en las investigaciones de la ACA (American Chain Association, Asociación Norteamericana de Cadenas). Estas ecuaciones pueden dar como resultado capacidades de potencia distintas a las publicadas por los fabricantes de cadenas para sus propias cadenas.
Por norma general, las ecuaciones de potencia de cadenas proporcionan la capacidad de potencia válida para transmisiones por cadena que funcionan en condiciones normales específicas. Si su transmisión por cadena funciona en condiciones anormales, el generador ajusta automáticamente los factores de potencia según sea necesario.
Para obtener más información sobre los factores de potencia, consulte el capítulo Conceptos básicos de cálculo. Se calculan a partir de usos habituales y condiciones normales de funcionamiento.
La capacidad de potencia de las transmisiones por cadena en condiciones normales de funcionamiento está limitada por:
- Fatiga de las placas de eslabón P R1
- La fatiga del impacto del casquillo y del rodillo P R2
- La corrosión entre el casquillo y el pasador P R3
Ejemplos de ecuaciones de potencia de cadena
![]()
![]()

P RN = min (P R1 ; P R2 ; P R3 )
donde:
|
P R1 |
Capacidad de potencia de transmisión por cadena limitada por la fatiga de las placas de eslabón [hp] |
|
|
P R2 |
Capacidad de potencia de transmisión por cadena limitada por la fatiga del impacto del casquillo y del rodillo [hp] |
|
|
P R3 |
Capacidad de potencia de transmisión por cadena limitada por la corrosión del casquillo y los pasadores [hp] |
|
|
z S |
Número de dientes de la rueda dentada pequeña [-] |
|
|
n S |
Velocidad de la rueda dentada pequeña [rpm] |
|
|
p |
Paso de cadena [pulgadas] |
P D = P f 1 f 2 f 5 f 6 f 7
P RN = min (P R1 ; P R2 ; P R3 )
![]()
Presión en el área de contacto de la cadena
Durante la vida útil de la transmisión por cadena, la carga fluctuante de tracción actúa en las superficies de contacto entre los pasadores y los casquillos. Esto provoca una presión específica en el área de contacto de la cadena. Si esta presión supera el valor admisible en el área de contacto de la cadena, la vida útil de la cadena se puede reducir notablemente y se produce un error en la comprobación de resistencia. Para llevar a cabo la comprobación de resistencia correctamente, se utiliza la siguiente ecuación:
![]()
La cantidad de presión real en el área de contacto de la cadena se calcula a partir de la tensión máxima en el intervalo de la cadena mediante la fórmula:
![]()
La presión admisible en el área de contacto de la cadena viene determinada por
p 0 = p B0 . φ
donde:
|
p B |
Presión real en el área de contacto de la cadena [Pa] |
|
|
p B0 |
Presión específica admisible en el rodamiento de la cadena en condiciones normales de funcionamiento [Pa] |
|
|
p 0 |
Presión admisible en el área de contacto de la cadena en condiciones normales de funcionamiento [Pa] |
|
|
F Tmax |
Tensión máxima en el intervalo de la cadena especificado [N] |
|
|
A |
Área de contacto de la cadena [m 2 ] |
|
| φ |
Factor de construcción de cadena [-] |
|
| λ |
Factor de fricción específico [-] |
Análisis de vida útil esperada
El programa verifica la vida útil esperada para
- un alargamiento de la cadena dado t h
- el impacto de la fatiga de las placas de eslabón t hL
- la fatiga del impacto del casquillo y del rodillo t hR
La comprobación de resistencia se supera si la vida útil requerida es igual o inferior a la vida útil esperada.
![]()
Vida útil esperada para un alargamiento de cadena dado
Debido al desgaste, la cadena se alarga progresivamente durante su vida útil. Cuando el alargamiento de la cadena alcanza el 3%, la vida útil esperada se calcula mediante la siguiente ecuación empírica

donde:
|
t h3% |
Vida útil esperada para un alargamiento de cadena del 3% [hr] |
|
|
f C |
Factor de desgaste [-] |
|
|
f m |
Factor de tamaño específico de cadena [-] |
|
|
f k |
Factor de velocidad de cadena [-] |
|
|
X |
Número de eslabones de la cadena [-] |
|
|
v |
Velocidad de cadena [m/s] |
|
|
z 1 |
Número de dientes de la rueda dentada pequeña [-] |
|
|
z 2 |
Número de dientes de la rueda dentada pequeña [-] |
|
|
p |
Paso de cadena [m] |
|
|
d 2 |
Diámetro del pasador de la cadena [m] |
|
|
p B |
Presión en el área de contacto de la cadena [N/cm 2 ] |
La transmisión por cadena con tres o más ruedas dentadas se sustituye por transmisiones de cadena virtuales formadas solo por dos ruedas dentadas. La vida útil resultante se calcula del modo siguiente. La presión en el área de contacto de la cadena depende específicamente del intervalo especificado en cada transmisión por cadena virtual.
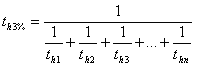
donde:
|
t h3% |
Vida útil esperada de la transmisión por cadena para un alargamiento de cadena del 3% [hr] |
|
|
t h1 ... t hn |
Vida útil esperada de la transmisión por cadena virtual para un alargamiento de cadena del 3% [hr] |
La vida útil esperada para elongaciones que no sean del 3% se calcula mediante la fórmula
![]()
donde:
|
t h3% |
Vida útil esperada de la transmisión por cadena para un alargamiento de cadena del 3% [hr] |
|
|
t h |
Vida útil esperada de la transmisión por cadena para un alargamiento de cadena determinado [hr] |
|
|
ΔL max |
Alargamiento máximo de la cadena [-] |
Factor de desgaste f C
El factor de desgaste tiene en cuenta la calidad de la lubricación y su impacto en el avance del desgaste de la cadena. El valor del factor de desgaste se determina en el siguiente gráfico con respecto al valor del factor de lubricación f 4 y la presión de en el área de contacto p B .

Factor de tamaño específico de cadena f m
El factor de tamaño de cadena tiene en cuenta el tamaño de la cadena y cómo éste afecta al avance del desgaste. El tamaño del factor se calcula a partir de la tabla siguiente.
|
Paso [mm] |
4 |
5 |
6 |
6,35 |
8 |
9,525 |
12,7 |
15,875 |
19,05 |
25,4 |
31,75 |
38,1 |
44,45 |
50,8 |
63,5 |
76,2 |
|
f m [-] |
1,64 |
1,57 |
1,54 |
1,53 |
1,49 |
1,48 |
1,44 |
1,39 |
1,34 |
1,27 |
1,23 |
1,19 |
1,15 |
1,11 |
1,03 |
0,96 |
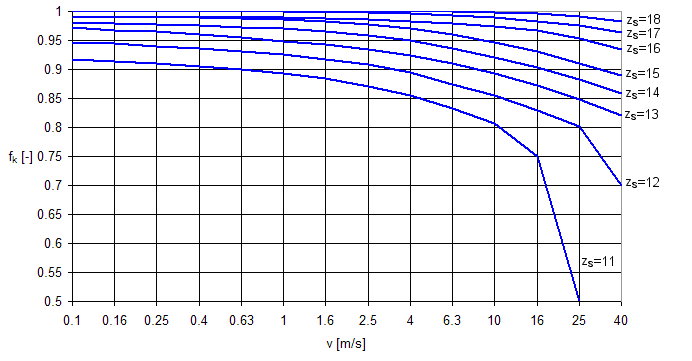
Factor de velocidad de la cadena f k
El factor de velocidad de la cadena tiene en cuenta la velocidad de la cadena v [m/s] para un número específico de dientes de la rueda dentada más pequeña z s [-]. Si la rueda dentada más pequeña de la transmisión tiene 19 dientes o más, el factor siempre es uno. Si la rueda dentada más pequeña tiene menos de 19 dientes, el factor de velocidad se obtiene del gráfico siguiente.
Vida útil esperada a causa de la fatiga de las placas de eslabón
La vida útil esperada sin errores de fatiga de las placas de eslabón se calcula mediante la siguiente fórmula empírica

donde:
|
t hL |
Vida útil esperada debido a la fatiga de las placas de eslabón [hr] |
|
|
X |
Número de eslabones de la cadena [-] |
|
|
n S |
Velocidad de la rueda dentada más pequeña [rpm] |
|
|
f Z |
Factor de los dientes [-] |
|
|
f Y |
Factor de tamaño específico de cadena [-] |
|
|
f 1 |
Factor de servicio [-] |
|
|
F U |
Resistencia máxima a tracción de la cadena [N] |
|
|
F P |
Tracción efectiva de cadena o carga de tracción [N] |
Factor de dientes f Z
El factor de dientes tiene en cuenta la modificación de la vida útil provocada por el tamaño de la rueda dentada más pequeña de la transmisión por cadena. El tamaño del factor se define mediante el siguiente gráfico.

Factor de tamaño específico de cadena f Y
Este factor tiene en cuenta el tamaño de la cadena en relación con los picos de sobrecarga. El tamaño del factor se define mediante el siguiente gráfico.

Vida útil esperada a causa de la fatiga del impacto del casquillo y del rodillo
La vida útil esperada sin errores de fatiga del impacto del casquillo y del rodillo se define mediante la siguiente ecuación empírica:

donde:
|
t hR |
Vida útil esperada debido a la fatiga del impacto del casquillo y del rodillo [hr] |
|
|
X |
Número de eslabones de la cadena [-] |
|
|
z S |
Número de dientes de la rueda dentada más pequeña [-] |
|
|
n S |
Velocidad de la rueda dentada más pequeña [rpm] |
|
|
f 1 |
Factor de servicio [-] |
|
|
f 3 |
Factor de cadena [-] |
|
|
P |
Potencia [W] |
|
|
d 1 |
Diámetro del rodillo de la cadena [m] |
|
|
d 2 |
Diámetro del pasador de la cadena [m] |
|
|
p |
Paso de cadena [m] |