Quadrilateral Plate Element Connection
Description: Defines a quadrilateral, isoparametric membrane-bending or plane strain plate element with vertex rotations.
Format:

Example:

| Field | Definition | Type | Default |
|---|---|---|---|
| EID | Element identification number. | Integer > 0 | Required |
| PID | Identification number of a PSHELL or PCOMP property entry. | Integer > 0 | Required |
| Gi | Grid point identification numbers of connection points. | Integer > 0 all unique | Required |
| THETA | Material property orientation angle in degrees. | Real | |
| MCID | Material coordinate system identification number. | Integer ≥ 0 | See Remark 7 |
| Ti | Membrane thickness of element at G1, G2, G3, and G4. | Real | See Remark 8 |
Remarks:
- Element identification numbers must be unique with respect to all other element identification numbers.
- Grid points G1 through G4 must be ordered consecutively around the perimeter of the element.
- All the interior angles must be less than 180°.
- Components of stress are output in the surface coordinate system. (See the SURFACE command in Section 3, Case Control.)
- The rotational degrees of freedom at the connection points and normal to the element are active in the element formulation and must not be constrained unless at a boundary. If they are constrained, then inaccurate results will be generated.
- This element is less sensitive to initial distortion and Poisson's ratio than the CQUAD4 element and is more compatible with the CBAR and CTRIAR elements that also have 6 degrees of freedom per node.
- If THETA/MCID is blank, field 5 of the PSHELL continuation entry will be used. If this field is also blank, then THETA = 0.0 is assumed when a non-isotropic material is referenced.
- If Ti in fields 4 through 7 of the continuation entry is blank, field 4 of the PSHELL entry will be used. This is the preferred way of specifying element thickness if the thickness does not vary over the element.
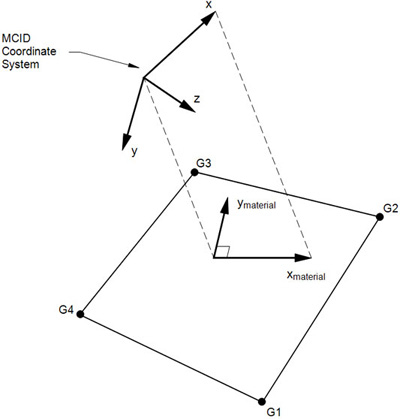
Figure 1. MCID Coordinate System Definition
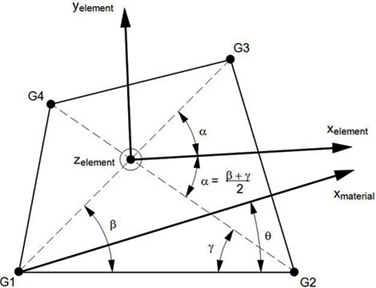
Figure 2. CQUADR Element Geometry and Coordinate System
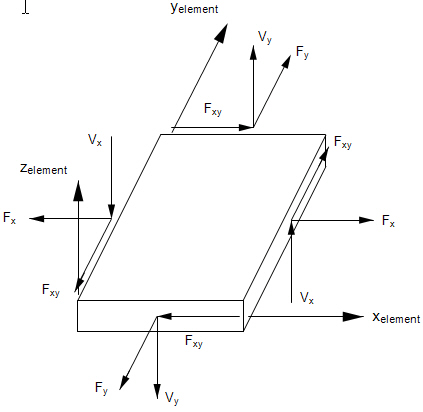
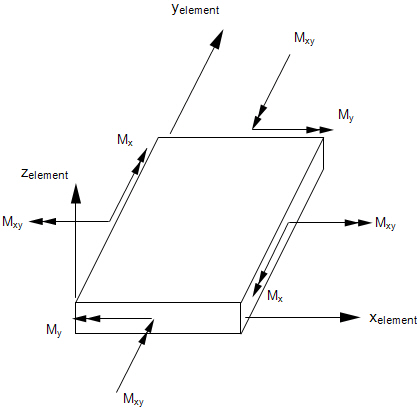
Figure 3. Forces and Moments in CQUADR Elements
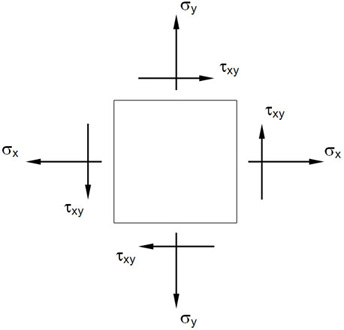
Figure 4. Stresses in CQUADR Elements