Pressão do solo – Algoritmos de cálculo de pressão

Os cálculos são executados de acordo com a teoria da cunha de falha de Coulomb.

Pressões do solo

Podem ser identificados os três modos característicos (limite) de ações do solo (pressões) indicados a seguir em uma estrutura de retenção:

• Pressão estática Po – Se um elemento de retenção não tiver sido deslocado
• Pressão ativa Pa – Se um elemento de retenção tiver sido deslocado, devido à ação de forças externas, na direção compatível com a pressão provocada pelo solo
• Pressão passiva Pp – Se um elemento de retenção tiver sido deslocado, devido à ação de forças externas, na direção oposta à pressão provocada pelo solo

A pressão está diretamente relacionada ao deslocamento de uma estrutura de retenção. O deslocamento é determinado usando a rotação do elemento ρ, que é definido como aproximadamente igual à relação f/H (deslocamento superior da parede/altura do elemento).

Pa <- ρ ≤ ρa

Po <- ρ = 0

Pp <- ρ ≥ ρp

Em que ρa e ρp são as pressões de limite para os modos correspondentes

Considera-se que existe uma relação linear entre as seguintes pressões:

Ka * P < Ko * P < Kp * P,

Em que P é uma determinada pressão, que no caso mais simples é equivalente à pressão hidrostática. As pressões intermediárias estão contidas entre as pressões de limite.

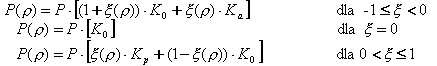
Em que ξ do intervalo <-1,1> corresponde à variável linearmente padronizada do intervalo <ρa, ρp>.

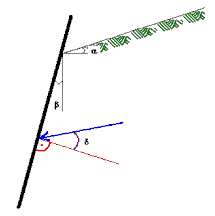
As pressões do solo dependem do peso da unidade do solo γ, do ângulo de inclinação natural ϕ, da inclinação de um elemento de retenção β e da inclinação de aterro α. O efeito do ângulo de atrito entre a parede e o solo δ é desconsiderado.

• A pressão hidrostática é igual ao peso do solo acima do plano que está sendo analisado. Para solos em camadas (n camadas acima de um determinado ponto), equivale a:
  
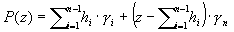
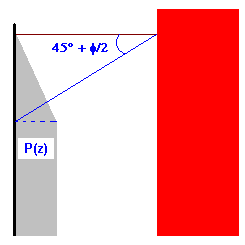
• A pressão é influenciada pela presença de outros objetos. Esse tipo de pressão ocorrerá se nas proximidades de um elemento de retenção houver outros objetos, que reduzem o valor da pressão do solo. Esse tipo de objeto impede que a pressão P(z) seja totalmente identificada com a pressão hidrostática. É equivalente à pressão hidrostática até que uma determinada profundidade zgr seja alcançada, depois a pressão P(z) fica constante:
  
  
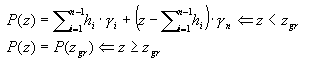
• A pressão estática é a pressão provocada pelo solo quando os deslocamentos do elemento de retenção atingem zero. Essa pressão é igual à pressão hidrostática multiplicada pelo coeficiente Ko: Po(z) = Ko * P(z), onde Ko = 1 - sinα.
• A pressão ativa é a pressão provocada pelo solo quando um elemento de retenção foi deslocado devido à ação de forças externas por um valor que é pelo menos igual ao valor limite ra na direção compatível com a pressão provocada pelo solo. Essa pressão é igual à pressão hidrostática multiplicada pelo coeficiente Ka: Pa(z) = Ka * P(z), em que
  
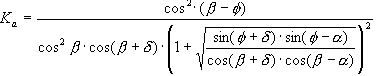
• A pressão passiva é a pressão provocada pelo solo quando um elemento de retenção foi deslocado devido à ação de forças externas por um valor que é pelo menos igual ao valor limite ρp na direção oposta à pressão provocada pelo solo. Essa pressão é igual à pressão hidrostática multiplicada pelo coeficiente Kp: Pp(z) = Kp * P(z), em que
  
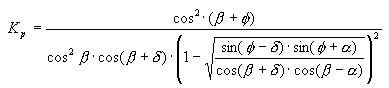
• As pressões intermediárias ocorrerão se o deslocamento do elemento de retenção estiver contido no intervalo ρa < ρ < ρp e ρ≠0. Trata-se de uma combinação entre pressão estática e pressão ativa ou passiva:
  

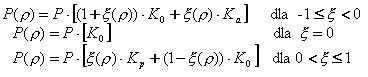
Pressões induzidas por cargas aplicadas à superfície do solo

Considera-se que a pressão resultante das cargas aplicadas ao solo é obtida multiplicando-se a pressão P'(z) pelo coeficiente K apropriado (Ko, Ka, Kp ou a combinação entre eles), de forma análoga à pressão do solo.

Dependendo da norma selecionada, os seguintes métodos e fatores de distribuição de carga são usados:

Uniforme

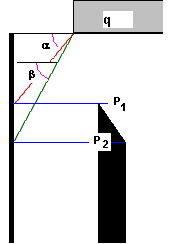
PN-83/B-03010: α=Φ, β=45+Φ/2 e P1= 0 e P2 =K q

PN-85/S-10030: α=Φ, β=45+Φ/2 e P1=K q e P2 =K q

SETRA (França): α=Φ, β=45+Φ/2 e P1= K q e P2 =K q

RD 31.31.27-81 (Rússia): sem algoritmo

Linear

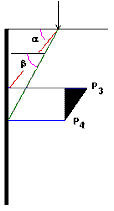
PN-83/B-03010: α=Φ, β=45+Φ/2 e P3= K Q e P4 =0

PN-85/S-10030: α=Φ, β=45+Φ/2 e P3= K Q e P4 =K Q

SETRA (França): α=Φ, β=45+Φ/2 e P3= K Q e P4 =K Q

RD 31.31.27-81 (Rússia): α=45+Φ/2, β=45+Φ/2 e P3= K Q e P4 =K Q

Uniformemente distribuído

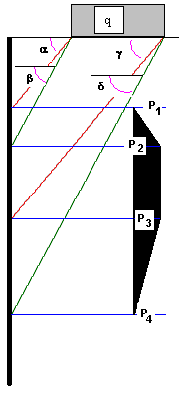
PN-83/B-03010: α=γ=Φ, β=δ=45+Φ/2 e P1=P4=0 e P2=P3=K q

PN-85/S-10030: α=Φ, β=45+Φ/2 e P1=P4= P2=P3=K q

SETRA (França): α=Φ, β=45+Φ/2 e P1=P4= P2=P3=K q

RD 31.31.27-81 (Rússia): α=45+Φ/2, β=45+Φ/2 e P1=P4= P2=P3=K q

Coesão do solo

As forças de coesão do solo são ignoradas ao calcular a pressão do solo. A coesão nem sempre é levada em conta nos cálculos, porque tem um efeito favorável nas estruturas. É uma força que faz com que uma escavação seja preservada mesmo sem um elemento de retenção. A coesão atua na direção oposta ao deslocamento de um elemento de retenção, reduzindo, assim, a ação do solo em uma parede. Um valor de pressão devido à coesão é constante para um determinado solo e é igual a:

Em que c indica a coesão do solo e o coeficiente Kc é igual a:

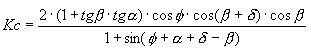
A coesão é considerada apenas para solos coesos.