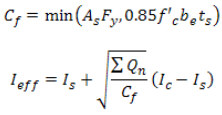Прогибы балки необходимо проверять в двух случаях: при нагрузке на конструкцию с прочностью несоставных балок и при полном комбинированном изгибе под эксплуатационной нагрузкой. Если выбран выгиб, это повлияет на результаты расчета изгибов.
Выгиб
При выборе выгиба его параметры рассчитываются до вычисления прогибов. Затем эти параметры используются для расчета истинных прогибов под воздействием эксплуатационных нагрузок. По умолчанию 80 % прогибов конструкции от собственного веса являются выгнутыми, а минимумы, максимумы и размеры шага устанавливаются пользователем. Поскольку прогибы могут быть нерегулярными, а максимум не всегда приходится на середину балки, параметры выгиба можно рассчитать для любой точки балки с тем условием, что выгиб балки проходит по дуге окружности. Радиус дуги r определяется, исходя из значения выгиба c и длины балки l:
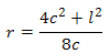
Далее выгиб для любого смещения x вычисляется по формуле:
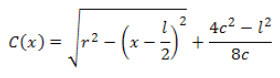
Прогибы конструкции
Во время строительства жесткость (следовательно, и прогиб) сечения обеспечивается только за счет несоставных стальных профилей. Для каждой балки рассчитываются прогибы под собственным весом плиты, вес стального сечения и любые другие нагрузки на конструкцию. Затем результаты сравниваются с предельными значениями, заданными пользователем. Для расчета прогиба используются значения жесткости E и момент инерции I стального сечения.
Если балка должна быть выгнутой, то сначала рассчитывается выгиб. Прогиб в точке определяется как выгиб в этой точке, вычитаемый из деформации балки под заданными нагрузками. Эти значения вычисляются с учетом эксплуатационных (нормативных) нагрузок. Учитываются следующие типы нагрузок:
- постоянные нагрузки на конструкцию (дополнительные нагрузки сверх собственного веса конструкции);
- временные нагрузки на конструкцию (дополнительные);
- собственный вес материалов.
Для предельных прогибов конструкции можно задать либо абсолютное значение (по умолчанию 2 дюйма), либо относительный коэффициент (по умолчанию L/500).
Эксплуатационные прогибы
Прогибы балки под эксплуатационными нагрузками оцениваются по двум критериям:
- общий прогиб под эксплуатационными постоянными и временными нагрузками (комбинированными);
- прогиб под эксплуатационными временными нагрузками.
Прогибы под временными нагрузками
В этом случае рассчитываются прогибы только под временными нагрузками. В расчете не учитывается выгиб. Эта проверка позволяет представить дифференциальное перемещение балки во время эксплуатации и учитывает только жесткость и момент инерции составного сечения (метод вычисления жесткости бетонного профиля см. ниже). Параметры прогибов под временными нагрузками ограничены абсолютным значением (по умолчанию 2 дюйма) и относительным значением (по умолчанию L/360), которые задаются пользователем.
Прогибы под комбинированными нагрузками
В этом случае значение максимального прогиба определяется как значение общего прогиба под всеми эксплуатационными нагрузками минус значение выгиба балки. Это позволяет вычислить провес балки относительно осевой линии в любой точке по всей длине. Однако, поскольку прогиб под собственным весом возникает при несоставных действиях, а прогиб под временными нагрузками — при составных, значения жесткости и момента инерции балок отличаются в каждом конкретном случае. Их необходимо рассчитывать по отдельности. Поэтому общий прогиб в этом случае равен сумме прогибов конструкции под собственным весом (значения I и E для стальных конструкций) и прогибов под всеми остальными нагрузками (значения I и E для составного сечения) за вычетом выгиба (рассчитанного на основе процентного соотношения прогибов под собственным весом). Параметры прогибов под комбинированными нагрузками ограничены абсолютным значением (по умолчанию 2 дюйма) или относительным значением (по умолчанию L/240).
Момент инерции составного сечения
Для вычисления прогибов конструкции под собственным весом требуется узнать расчетный момент инерции на основании свойств упругости составного сечения. Они определяются, исходя из геометрии профиля и (для частично составных действий) процентного значения полностью составного действия, характерного для упоров. Ползучесть бетона от длительной нагрузки в этом расчете не учитывается.
На первом этапе необходимо определить, где проходит упругая нейтральная ось (E.N.A): по плите или стальному сечению. Это можно сделать с помощью следующих расчетов. В зависимости от условий преобразованный момент инерции упругого составного сечения вычисляется с помощью метода Чэу (1996).
Если
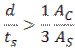
ось E.N.A. проходит через стальной профиль:
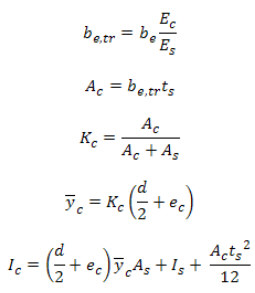
Если
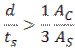
ось E.N.A. проходит через плиту:
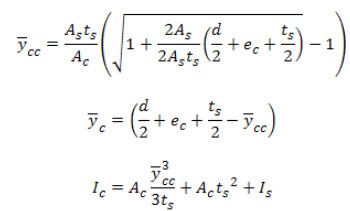
Где:
E c / Es = n — коэффициент модульной жесткости
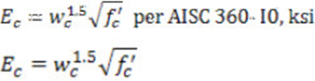
Y c — расстояние от центра тяжести стального сечения до упругой нейтральной оси
ec — расстояние от верхней полки стального сечения до центра тяжести приведенной бетонной полки
Is — момент инерции стального сечения
Ic — преобразованный момент инерции полностью составного сечения
Расчетный момент инерции для частично составного сечения, I eff (который используется для вычисления всех прогибов под эксплуатационных нагрузках), рассчитывается по формуле C-I3-3 из комментария к ANSI/AISC 360-10 на основе отношения прочности упоров (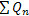
) к усилию сжатия полки полностью составного сечения Cf:
