之前我们看到了显示材料如何展示压缩下的载荷降低的实验数据。我们把此载荷降低的幅值称为 μ。μ 值会随载荷角度的更改而改变。因此，我们需要一种方法来确定触发压缩失效准则的任意应力状态的 μ。

0°：

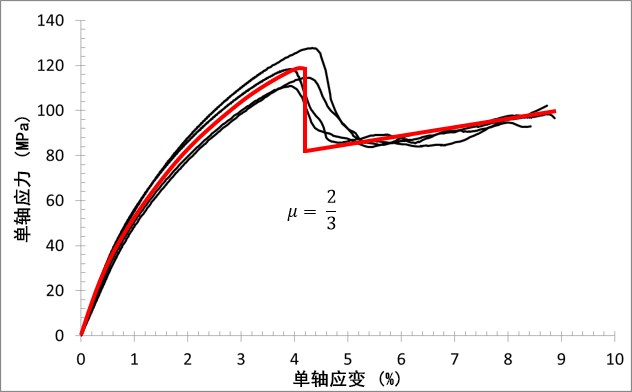
90°：

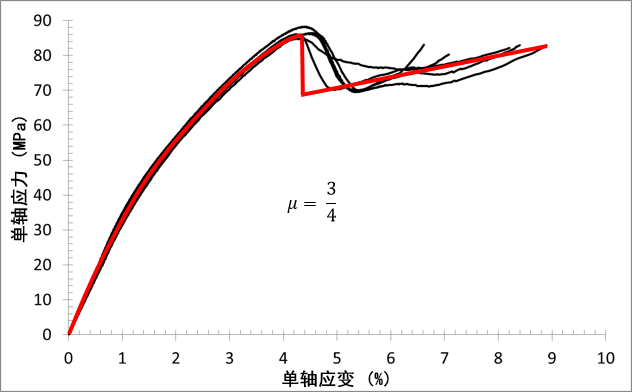
45°：

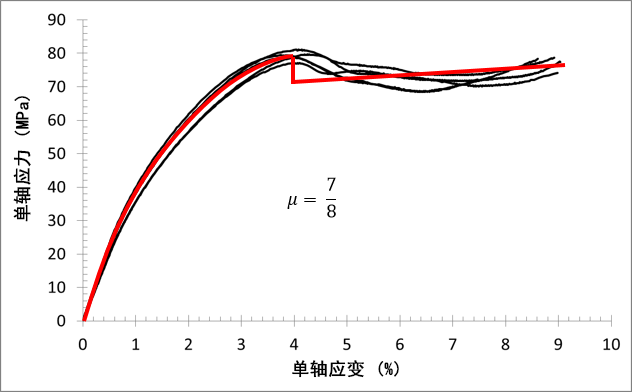
确定 μ

第一步是要确定触发压缩失效准则的基体应力状态的主应力 (σI ≥ σII ≥ σIII) 和主方向 (âI, âII, âIII)。第三个主应力 (σIII) 将始终是幅值最大的压缩应力。 接下来，我们确定第三个主方向 (âIII) 和主材料方向的角度。 我们将此角度表示为 ξ。

现在，我们将 μ 作为角度的二次函数写入。

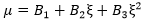
其中，系数 B1、B2 和 B3 取决于三个实验应力-应变响应中的载荷下降。通过将三个已知输入角度 ξ (0, 90, 45) 和测得的载荷下降 μ 用于每条曲线，我们可以求解方程组来确定系数 B1、B2 和 B3。这些系数在结构分析期间使用，以确定应用于触发压缩失效准则的任意给定应力状态的相应载荷降低。

下图显示了相对于主纤维方向，μ 如何依赖于主压缩应力方向的示例。

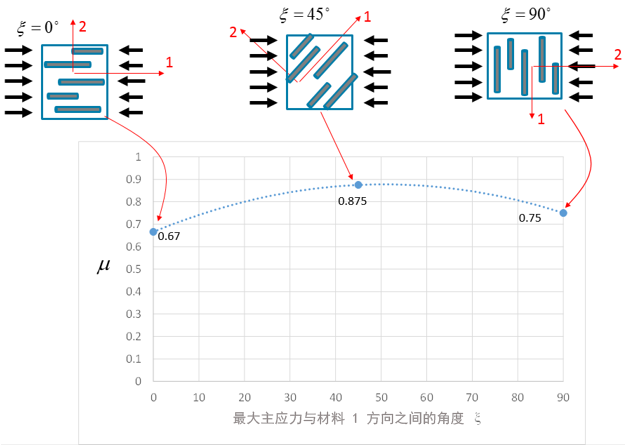
损坏演变

在确定用于触发失效的应力状态的 μ 后，我们可以将其用于复合应力。复合材料的刚度在由刚度基体乘以分数 μ 后会瞬时缩减。在应用 μ 后，塑性响应会像之前那样继续演变。