Mit der Funktion nor lässt sich der normale Einheitsvektor berechnen (ein Vektor, der senkrecht zu einer Linie oder Ebene steht), nicht ein Punkt. Der Vektor definiert die Richtung der Normale, keine Position im Raum. Sie können diesen Einheitsvektor zu einem Punkt addieren, um einen anderen Punkt zu bestimmen.
- nor
-
Bestimmt den dreidimensionalen Normaleneinheitsvektor eines ausgewählten Kreis-, Bogen- oder Polylinien-Bogensegments. Dieser Normalenvektor bezeichnet die Z-Koordinate des Objektkoordinatensystems (OKS) des ausgewählten Objekts.
- nor(v)
-
Legt für den zweidimensionalen Normaleneinheitsvektor den Vektor v fest. Beide Punkte werden als zweidimensional betrachtet und in die XY-Ebene des aktuellen BKS projiziert. Der resultierende Normalenvektor ist so orientiert, dass er vom Ausgangsvektor v nach links zeigt.
- nor(p1,p2)
-
Liefert den zweidimensionalen normalen Einheitsvektor zur Linie P1,P2. Die Linie verläuft von P1 zu P2. Der resultierende Normalenvektor ist so orientiert, dass er von der Ausgangslinie (P1,P2) nach links zeigt.
- nor(p1,p2,p3)
-
Liefert den dreidimensionalen normalen Einheitsvektor zu der Ebene, die von den drei Punkten P1, P2 und P3 aufgespannt wird. Die Normale ist so orientiert, dass die gegebenen Punkte bezogen auf den Normalenvektor entgegen dem Uhrzeigersinn angeordnet sind.
In den folgenden Abbildungen wird dargestellt, wie normale Vektoren berechnet werden:
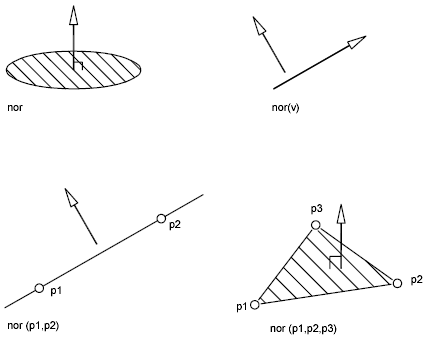
Im folgenden Beispiel wird die Ansichtsrichtung senkrecht zu einem ausgewählten Objekt gesetzt. Das Programm stellt das Objekt in der Draufsicht dar. Eine Verzerrung durch Parallelprojektion findet nicht statt.
Befehl: apunkt
Aktuelle Ansichtsrichtung: VIEWDIR=aktuell
Ansichtspunkt angeben oder [Drehen] <Kompass und Achsen anzeigen>: 'kal
>> Ausdruck: nor
>> Kreis, Bogen oder Polylinie für die Funktion NOR auswählen: