Lösungsmethode
Alle der oben genannten zugrunde liegenden PDEs werden anhand der zuvor beschriebenen Finites-Element-Methode diskretisiert. Der resultierende Satz algebraischer Gleichungen muss gelöst werden, um die Werte von abhängigen Variablen an den Knoten der finiten Elemente zu ermitteln. Der von Autodesk® CFD verwendete Algorithmus zur Lösung dieser Gleichungen wird in diesem Abschnitt beschrieben.
Abgetrennter Solver
Das erste Problem, das beim Lösen der diskretisierten Gleichungen zu beheben ist, betrifft den fehlenden Druck. Wenn die Impulsgleichungen zur Berechnung der Geschwindigkeitskomponenten herangezogen werden, muss die Kontinuitätsgleichung zur Ermittlung des Drucks verwendet werden. Der Druck geht jedoch niemals explizit in die Kontinuitätsgleichung ein. Es gibt zahlreiche Möglichkeiten, um die numerischen Schwierigkeiten mit der impliziten Druckkopplung zu umgehen. Für viele dieser Lösungsmethoden ist es erforderlich, dass die Kontinuitäts- und die Impulsgleichungen an jedem Knoten des FE-Netzes gleichzeitig gelöst werden. Für kleinere Probleme ist diese Lösung relativ gut geeignet. Für die meisten Probleme aus dem wirklichen Leben stellt diese Lösung jedoch eine starke Belastung für Computerressourcen dar und kann sogar eine Lösung für ein Problem verhindern. Um dieses Manko zu mindern, muss eine explizite Gleichung für den Druck gefunden werden.
Die von Autodesk® CFD gelöste Druckgleichung wird von der Kontinuitätsgleichung abgeleitet. Das gewichtete Integral der Kontinuitätsgleichung wird herangezogen, wenn die Integration nach Teilen zur Reduzierung der Ordnung der Integration verwendet wird:
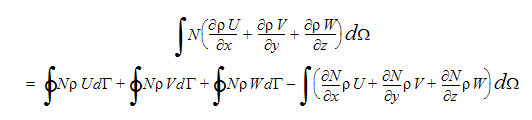
Die ersten drei Integrale auf der rechten Seite dieser Gleichung stellen den Massenfluss über Elementbegrenzungen hinweg dar. Diese Integrale werden an den Elementinnenflächen abgebrochen und sind null für alle Begrenzungen, über die keine Masse fließt (Symmetrie, Wände). Damit stellen diese Terme die natürliche Randbedingung für die Druckgleichung dar.
Um das Auftreten von Druck in dieser Gleichung zu erzwingen, muss eine Beziehung zwischen Geschwindigkeit und Druck abgeleitet werden. Diese Beziehung kann aus den Impulsgleichungen hergeleitet werden. Mit einer halbdiskretisierten Form der Impulsgleichungen lässt sich die Beziehung zwischen Geschwindigkeit und Druck wie folgt ausdrücken:
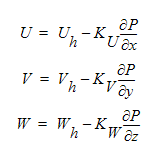
In diesen Gleichungen enthalten die Terme Uh, Vh, Wh alle nicht auf der Diagonalen liegenden Terme in den Impulsgleichungen. Wenn diese drei Gleichungen nun in die vorherige Kontinuitätsgleichung eingebracht werden, ergibt sich die folgende Druckgleichung:
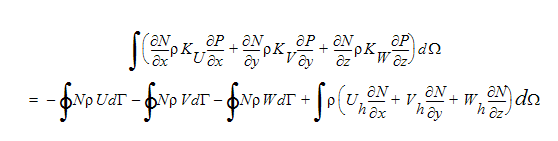
Beachten Sie, dass diese Gleichung in der diskretisierten Form der Poisson-Gleichung vorliegt und daher eine symmetrische Koeffizientenmatrix erzeugt.
Für kompressible Strömungen muss die Dichte-Druck-Kopplung ebenfalls berücksichtigt werden. Dieser Kopplung wird durch Verwendung des folgenden Ausdrucks Rechnung getragen:
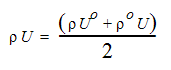
"o" bezieht sich hierbei auf alte Werte. Dieser Ausdruck wird verwendet, wenn die Kontinuitätsgleichung nach Teilen integriert wird. Durch Ersetzen der Geschwindigkeit ergibt sich Folgendes:
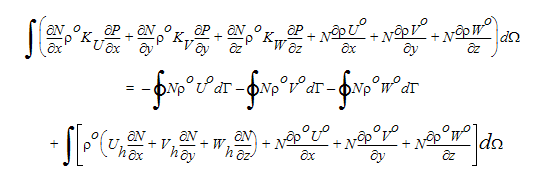
Die zusätzlichen advektionsähnlichen Terme auf der linken Seite dieser Gleichung werden anhand des idealen Gasgesetzes mit Hinblick auf den Druck neu verfasst. Mit diesen zusätzlichen Advektionstermen führt die Gleichung für kompressiblen Druck zu einer nichtsymmetrischen Koeffizientenmatrix, ähnlich wie bei den anderen Transportgleichungen.
Mit einer expliziten Druckgleichung lässt sich jede der zugrunde liegenden Gleichungen separat lösen. Dies bedeutet, dass die x-Impulsgleichung für U an allen Knoten, die y-Impulsgleichung für V an allen Knoten, die z-Impulsgleichung für W auf allen Knoten, die Druckgleichung für P an allen Knoten usw. gelöst werden kann. Dies ermöglicht einen wesentlich geringeren Speicherbedarf, da nur jeweils ein Freiheitsgrad gelöst wird. Dieser Ansatz wird als abgetrennter Solver bezeichnet, da jede der abhängigen Variablen separat gelöst wird. Darüber hinaus müssen lediglich die Terme ungleich Null in der Koeffizientenmatrix gespeichert werden, da jede dieser Gleichungen anhand iterativer Matrixverfahren gelöst werden kann.