The characteristics of modal, seismic and seismic (pseudo) structure analysis modes are shown below.
Modal Mode
This is approach allows the modal analysis of the structure, setting the first n values and eigenvectors of the structure.
The available analysis methods: subspace iteration, Lanczos method and the basis reduction method.
Iterations will be completed if the following condition is met:
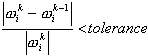
where: i = 1,2,...,n vibration modes, k - number of iterations.
Upper limit is the period value (pulsation, frequency), which describes that in the range, (0, upper limit) the following values and eigenvectors will be set.
Sturm check, which allows finding the skipped pulsations, is possible.
Seismic Mode
For seismic and spectral structure analysis it is not essential that the values and eigenvectors be arranged in order. It is important that only values and eigenvectors characterized by a large mass participation coefficient (having a large effect on the seismic response) be taken into consideration.
In this mode, n values and eigenvectors of the structure are set. The set values are not arranged in order and some values and vectors may be omitted.
Available analysis methods: Lanczos method.
Convergence method:

where:
Φ i - i-th eigenvector
Upper limit where limits are ignored.
Sturm check is not performed for this structure analysis mode.
Seismic (pseudomodal) Mode
This mode is used only for a spectral and seismic analysis. It should be for classic analysis methods based on modal decomposition results in very long structure analysis times. This method consists of presenting the X solution vector as a superposition of certain base vectors which are not the exact approximation of the Φ i mode.
Available analysis methods: Lanczos method.
Sturm check is not performed for this structure analysis mode.
When in a program a Lanczos' method is selected, the program changes a calculation method to a subspace iteration method. To use the Lanczos' method in calculations, separated structures should be connected in such a way that a structure model is not changed (for example, a bar among the supports should be added).