Compressible Flow
When a fluid flow is compressible, the fluid density varies with its pressure. Compressible flows are usually high speed flows with Mach numbers greater than about 0.3. Examples include aerodynamic applications such as flow over a wing or aircraft nacelle as well as industrial applications such as flow through high-performance valves.
Incompressible flows do not have such a variation of density. The key differentiation between compressible and incompressible is the velocity of the flow. A fluid such as air that is moving slower than Mach 0.3 is considered incompressible, even though it is a gas. A gas that is run through a compressor is not truly considered compressible (in the thermodynamic sense) unless its velocity exceeds Mach 0.3. This is important to note because analyses run as compressible can be harder to run, and require more longer analysis times than incompressible flows.
In Autodesk® CFD, the distinction between subsonic compressible and full compressible is based on the Mach number.
Subsonic compressible flows have a Mach number between 0.3 and 0.8. The relationship between pressure and density is weak, and no shocks will be computed within the flow.
Compressible flows have a Mach number greater than 0.8. The pressure strongly affects the density, and shocks are possible. Compressible flows can be either transonic (0.8 < M < 1.2) or supersonic (1.2 < M < 3.0). In supersonic flows, pressure effects are only transported downstream. The upstream flow is not affected by conditions and obstructions downstream.
The speed of sound is given as a:
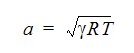
Where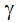 
=1.4 for air, R = gas constant, and T = reference static temperature (in absolute units).
The velocity, V, is then the product of the sound speed, a, and the Mach number, M:
The total temperature, Tt, is a key parameter as well, and is the sum of the static temperature and the dynamic temperature. There are two way to calculate total temperature:
- V is the velocity
- Cp is the gas specific heat
For air, Cp = 1005 m2/(s2 K)
Note that the total temperature must be specified as a constant value for analyses that do not have heat transfer and as a boundary condition for those that do.
The total pressure, Pt, is another useful quantity for running compressible analyses. It is the sum of the static pressure and the dynamic pressure.
If the flow accelerates through a geometrically converging section to sonic speed, the flow is considered to be choked. When choked, no additional mass can pass through the constriction region, even as the pressure drop is increased (by lowering the outlet back pressure). The flow downstream of the throat can then expand and become supersonic.
Basic Solution Strategy
Compressible flow analyses are much more sensitive to the applied boundary conditions and material properties than incompressible analyses. If the applied settings do not define a physically real flow situation, then the analysis can be very unstable and may fail to reach a converged solution.
For this reason, we recommend that you understand the flow situation that you are trying to analyze. Proper specification of the boundary conditions and material properties will greatly improve the chances of a successful analysis.
Test-Runs
A technique that can be very helpful when starting a new analysis is to mock up a two dimensional representation of the model to ensure that all conditions are correct. Inconsistent settings will be revealed very quickly as a 2D model is run, allowing for much faster debugging of the analysis. When the settings properly define the analysis, they can be applied to the (usually) much bigger 3D (or more detailed 2D) model with confidence that any additional adjustments to the model have to be made to the mesh and not the fundamental set-up.
Meshing
To capture physical elements such as shocks, the mesh size will have to be quite fine in critical areas. The mesh can be less fine in non-critical areas. A good guideline governing mesh transition is that the mesh size should not transition by more than a factor of four between neighboring fluid volumes. In general, a coarse mesh will be more stable but less accurate. For this reason, as part of the test procedure described above, in some cases it is recommended to verify the analysis set-up with a coarse mesh, and then when you are confident in your settings, refine the mesh to improve accuracy.
Materials
To allow the density to vary, open the Material Environment dialog, and select Variable. If the operating conditions are different from the default values, right click on the Material branch of the Design Study bar, and click Edit environment reference. Specify the appropriate static pressure and static temperature. Because the density is calculated using these values, the Environment pressure needs to be exact for the gage reference point to be correct.
Heat Transfer
To include heat transfer in a compressible analysis, apply Total (stagnation) temperature boundary conditions instead of static temperatures at the inlets. Total temperature should also be applied to any solids or walls with known temperature conditions. (Do not use a Static Temperature boundary condition to define a known temperature in a compressible analysis. At a wall the value of static and total temperature is the same, and should be applied as a total temperature.) The Set Heat Transfer to On in the Solve dialog. The value of Total Temperature on the Solve dialog will be ignored if heat transfer is enabled.
Note that when heat transfer is present in a compressible analysis, viscous dissipation, pressure work, and kinetic energy terms are calculated. It is only necessary to enable heat transfer if you are solving for heat transfer or for flow velocities higher than M = 3.0 if viscous dissipation is important or to capture a very crisp shock.
It is very important that the total temperature is specified correctly. A good test is to run zero iterations and check that the Mach number at the inlet is the expected value. If not, adjust the total temperature and inlet boundary conditions accordingly.
If heat transfer is not solved for, it is necessary to specify a Total temperature in the Solve dialog. The equation for total temperature is given above.
Absolute, Total, Static and Dynamic Values
The term absolute is used in conjunction with pressure. Normally, the solution to the pressure equation is a relative pressure. This relative pressure does not contain the gravitational head or the rotational head or the reference pressure. It is the part of the pressure that is affected by the velocities in the momentum equation directly. The absolute pressure adds the gravitational and rotational heads and the reference pressure to that calculated from the pressure equation. Referring to the relative pressure as Prel, the absolute pressure is calculated as:
where the ref subscript refers to reference values, the subscript i refers to the 3 coordinate directions, g is the gravitational acceleration and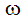 
is the rotational speed. The reference density is calculated at the beginning of the analysis using the reference pressure and temperature. For flows with a constant density, the reference density is the constant value. For flows which have no gravitational or rotational heads, the relative pressure is the gage pressure.
The terms dynamic and static are used most commonly with compressible fluids. The dynamic values are kinetic energy-like terms:
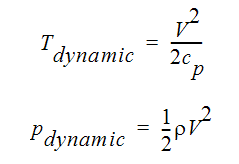
Note that the specific heat used to calculate the dynamic temperature is not the thermal value entered on the property window, but is a mechanical value calculated using:
where 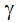is the ratio of the constant pressure specific heat to the constant volume specific heat and Rgas is the gas constant for this gas.
The static temperature is determined by solving the energy equation. For adiabatic properties, the energy equation that is used to determine the static temperature is the constant total temperature equation. Hence, the static temperature is the total or stagnation temperature minus the dynamic temperature.
The static pressure is the absolute pressure shown earlier. The total temperature is the sum of the static and dynamic temperatures. The total pressure is the sum of the static or absolute pressure and the dynamic pressure.
Related Topics:
Example Internal Compressible Flow Analysis