Principes adoptés dans l’analyse modale de la structure

L’analyse modale permet de calculer les valeurs propres et leurs valeurs connexes (pulsations propres, fréquences propres ou périodes propres), précision, vecteurs propres, coefficients de participation et masses participantes pour l’étude aux vibrations propres de la structure.

Dans le logiciel, trois modes d’analyse dynamique de la structure sont disponibles : modal, sismique et sismique pseudomodal.

Les modes propres de la structure et leurs valeurs sont calculées d’après l’équation :

(1)

où :

K - matrice de rigidité de la structure

M - matrice des masses de la structure

ω_i - pulsation propre (circulation propre) du mode "i",

U_i - vecteur propre du mode "i".

Le nombre de modes propres à prendre en compte peut être spécifié comme suit :

• par la limite supérieure de la pulsation, fréquence ou période
• par la limite inférieure du total des masses participantes (en pourcentage), ou de façon directe, par le nombre de modes propres exigés.

Si le nombre de modes n’a pas été défini, le nombre de modes par défaut défini dans les préférences sera pris en compte dans les calculs.

Les paramètres de contrôle de l'algorithme de problème aux valeurs propres sont les suivants.

• précision des calculs (valeur de l’erreur admissible)
• nombre maximal d’itérations

Les types de matrice des masses suivants sont disponibles.

• Cohérentes (matrice complète - les degrés de liberté en rotation sont toujours pris en compte)
• Concentrées avec rotations (matrice diagonale avec prise en compte des degrés de liberté en rotation)
• Concentrées sans rotations (matrice diagonale sans prise en compte des degrés de liberté en rotation)

Les matrices des masses cohérentes Mlum sont créées d’après le principe suivant :

Mlum(i,j) = 0.0 ; pour i≠j

Mlum(i,j) = Stot/Sdiag * M(i,j) ; pour i=j (2)

où :

Stot - total de tous les éléments de la matrice des masses complète M,

Sdiag - total des éléments appartenant à la diagonale principale de la matrice des masses M.

D’après les définitions données, il s’ensuit que la matrice de l’élément est préservée et définie de façon positive.

Les vecteurs propres présentés dans les résultats sont normalisés de façon que la composante maximale de chaque vecteur soit égale à 1.0.

Les vecteurs propres utilisés lors des calculs sont normalisés de sorte que la condition suivante soit satisfaite :

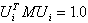(3)

La valeur de la précision donnée dans la boîte de dialogue des valeurs propres, définit la précision obtenue pour la convergence de la méthode. Cette valeur définit la mesure de l’erreur du calcul de la valeur propre λ_i et du vecteur propre U_i lors de l’itération pour le i-ème mode dans l’équation du problème aux valeurs propres donnée ci-dessous :

K * U_i = λ_i * M * U_i (4)

Les facteurs de participation sont définis de la façon suivante :

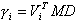
où :

D - vecteur unitaire défini de la façon suivante :

D(j) = 1.0 si "j" correspond au i-ème degré de liberté

D(j) = 0.0 si j ¹ i,

V_i - vecteur propre du mode "i" normalisé de sorte que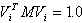

Les masses participantes sont des masses dynamiques participant dans le mouvement de la structure pour chaque déformée modale et pour chaque degré de liberté. Elles sont exprimées comme masses courantes (pour le mode propre actuel) et comme masses relatives. Une masse relative est définie comme étant la somme des masses courantes à partir du premier mode jusqu’au mode courant. Les valeurs sont affichées en pourcentage des masses dynamiques totales (celles-ci sont aussi calculées par le logiciel).

Les masses participantes actuelles sont définies comme suit :

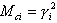
Actuellement, la méthode par défaut de résolution du problème aux valeurs propres est la méthode de Lanczos. La méthode de Lanczos est un excellent algorithme permettant la résolution des problèmes aux valeurs propres à grande échelle (1). Cette méthode permet d’obtenir n premiers vecteurs et valeurs propres recherchées avec une précision quelconque.

Pour la majorité des problèmes, la méthode de Lanczos est la méthode conseillée parmi les méthodes disponibles dans le système Robot. Néanmoins, cet algorithme présente les limitations suivantes :

• La matrice à trois diagonales T ne doit pas être du type cohérent.
• La matrice des masses M doit être traitée comme concentrée avec rotation ou cohérente. Lorsque l'option Concentrées sans rotation est sélectionnée, la matrice des masses est automatiquement agrégée sous la forme concentrée avec rotation.

Remarque : Pour les structures disjointes, il ne faut pas utiliser la méthode de Lanczos parce qu’elle exige la matrice à trois diagonales non décomposée T, alors que pour la structure disjointe la matrice T est cohérente.

Si vous avez choisi la méthode de Lanczos, le logiciel change automatiquement la méthode de calcul en méthode d’itération dans le sous-espace. Si vous voulez absolument utiliser la méthode de Lanczos, vous devez alors connecter les structures disjointes de façon à ce que le modèle de structure ne soit pas changé (p. ex. ajouter une barre entre les appuis).

La méthode de Lanczos utilise la réduction de la matrice à trois diagonales T. Ce procédé est représenté ci-dessous :

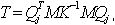
où :

Q_j = {q₁, q₂, ... , q_j} - matrice rectangulaire Neq x j, Neq - nombre d'équations, j - nombre de pas de Lanczos, q_j - j-th vecteur de Lanczos.

La formule

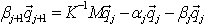
permet de créer le vecteur de Lanczos suivant q_j+1 et donne la ligne actuelle de la matrice T :

Par conséquent, le problème aux valeurs propres réduit est le suivant :

, k=1,2,…,j

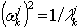, où ω_k ^j est la j-ème approximation ω_k, k=1,2,…,n, et n est le nombre requis de valeurs et de vecteurs propres. L’algorithme poursuivra le calcul (en augmentant j - nombre de pas de Lanczos) jusqu'à l’obtention de la précision demandée pour toutes les n valeurs propres.

La procédure d’orthogonalisation assure l’orthogonalité des vecteurs de Lanczos qj, ce qui garantit la sûreté et la stabilité numérique du procédé de calcul.

Les vecteurs propres doivent être obtenus à partir des formules suivantes :

U = Qs

Méthode de réduction de la base

Cet algorithme permet d’obtenir des valeurs approximatives des premières valeurs propres, si vous avez déjà certaines informations sur ces valeurs. La méthode demande la définition des degrés de liberté de type "maître" (MDOF - master degree of freedom) afin d’obtenir un système réduit. Par conséquent, vous avez la possibilité d’influer sur le procédure de création du modèle réduit. L’algorithme en question est un bon outil pour les utilisateurs expérimentés dans l’analyse dynamique et pour les cas où le comportement dynamique de la structure étudiée est connu. La méthode permet d’exclure du modèle réduit les degrés de liberté inutiles, ce qui fait que, après la suppression de ces degrés de liberté, la taille du système d’équations à résoudre est beaucoup moins importante.

Les règles suivantes s'appliquent à cette méthode.

• Les MDOF doivent être spécifiés : nœuds et directions de type "maître". On admet que les déplacements seuls peuvent être pris comme degrés de liberté de type "maître" (les rotations ne sont pas permises à cet effet).
• Tout type de matrice de masses peut être utilisé dans l'algorithme. Toutefois, le type de matrice Concentrées sans rotation garantit la période de calcul la plus courte.
• La vérification de Sturm indique le nombre de fréquences non détectées. Elle ne recherche pas ces valeurs et ces vecteurs propres. L'augmentation du nombre de MDOF afin de résoudre ce problème et comparer les valeurs propres est le seul moyen de déterminer la convergence de la vérification.

La méthode utilise la transformation du problème aux valeurs propres important pour le modèle MEF

K U - ω² M U = 0 au problème aux valeurs propres pour un modèle réduit :

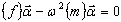
où {f} - matrice de l'influence, {m} - matrice généralisée pour le modèle réduit.

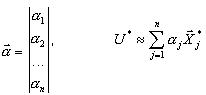
La base d’une telle transformation est constituée des solutions obtenues pour les états unitaires appropriés :

les forces nodales unitaires sont appliquées l’une après l’autre à chaque nœud de type "maître" dans la direction de type maître sélectionnée. Un problème statique de taille importante sera résolu pour "n" côtés droits :

K X_i ^* = T_i , i = 1, 2, …, n

où T_i est le vecteur de charge correspondant à la i-ème force unitaire. Vous devez définir les nœuds et les directions de type "maître", toutes les autres opérations seront effectuées par le logiciel. Le problème aux valeurs propres est ensuite résolu à l’aide de la méthode de Jacobi. Comme résultat, on obtient les valeurs approximatives de la fréquence w_i et de vecteurs propres U_i ^* , i=1,2,…,n.

Rubrique connexe :

Analyse modale - Précision des calculs dans l’analyse modale de la structure