Les solveurs itératifs sont utilisés dans des équations lorsque des méthodes de réorganisation des solveurs directs ne sont pas efficaces et que la matrice de rigidité K est suffisamment bien conditionnée.
Généralités
Les solveurs itératifs sont recommandés pour les problèmes importants correctement conditionnés (de 15 000 à 1 000 000 d'équations), pour les tâches linéaires statiques et les problèmes à valeur propre (analyse modale ou de flambement).
Les méthodes directes traditionnelles, c'est-à-dire les méthodes frontale, Skyline et fragmentée sont chronophages et requièrent une grande quantité d'espace disque disponible pour stocker une matrice factorisée.
Les solveurs itératifs, d'autre part, réduisent considérablement le temps de calcul et l'espace occupé sur le disque. Néanmoins, ils présentent quelques inconvénients :
- Leur convergence est lente si des problèmes mal conditionnés sont détectés.
- Chaque cas de charge est calculé de façon itérative depuis le début. Vous devez définir aussi peu de cas de charge que possible.
Les solveurs itératifs sont efficaces pour l'analyse de structures contenant un solide FE. Ils sont également utiles pendant les analyses statiques linéaires (recherche des paramètres de dimensionnement optimaux, par exemple), lorsqu'il est possible d'obtenir des solutions approximatives pour quelques cas de charge.
Le contrôle élément par élément de l'exactitude des données de régularisation Vinget constitue une application supplémentaire des solveurs itératifs, qui vous permettent de détecter des difficultés d'identification des erreurs dans le modèle FE.
La méthode PCG (gradient préconditionné) inclut plusieurs types de préconditionnement.
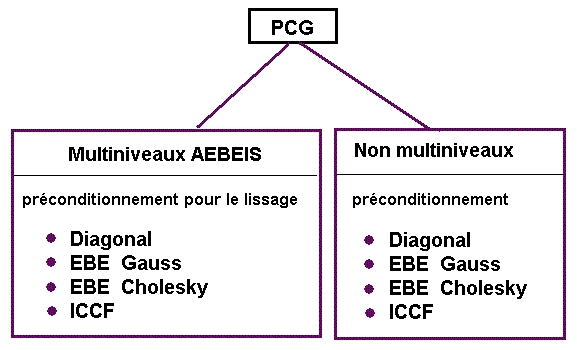
- AEBEIS : Agrégation - Solveur itératif élément par élément 1,2
- EBE : Elément par élément
- ICCF : Approche incomplète - factorisation Cholesky.
Méthode élément par élément (PCGEBE) et solveur itératif multiniveau (AEBEIS)
Le solveur PCGEBE est utilisé pour tous les types d'éléments finis, son utilisation n'étant pas limitée par la taille du problème. Il est cependant sensible au mauvais conditionnement de la matrice de rigidité K, ce qui peut ralentir la convergence.
AEBEIS est un solveur itératif multiniveau, d'agrégation, élément par élément, qui combine les avantages des méthodes d'itération rapide à la technique EBE économique. Il permet l'accélération d'opérations de base via une approche économique des exigences en termes de mémoire requise. Les méthodes de type agrégation comme celle-ci permettent d'effectuer une analyse des éléments solides et de coque (à l'instar des méthodes "multi-grid"), ainsi qu'une analyse des barres et des structures composées de barres, structures solides et en coques.
D'une manière générale, le solveur AEBEIS permet d'accélérer la convergence par rapport aux méthodes à un seul niveau. Il garantit une convergence stable pour les problèmes mal conditionnés, mais elle est moins sécurisée. Dans de rares cas, le préconditionnement est verrouillé, et la convergence est lente. Ce solveur a été implémenté en combinant le solveur d'agrégation sur la base de la technique EBE.
Le solveur AEBEIS permet l'application d'éléments de barre 2D et 3D, d'élément de coque (3, 4, 6 et 8 éléments de nœud) et d'éléments solides. Il permet également d'éléments de composants de structure supplémentaire comme des appuis élastiques, des décalages, des relâchements et les liaisons rigides. Il n'existe aucune restriction concernant les types d'élément ou de structure pour une méthode non-multiniveau.
Les types suivants de préconditionnement sont disponibles dans les deux approches AEBEIS et non-multiniveau.
- Diagonale - Préconditionnement Jacobi (ne s'applique qu'à des problèmes bien conditionnés).
- EBE Gauss - Préconditionnement EBE Gauss-Seidel-Cholesky modifié 12.
- EBE Cholesky - Préconditionnement EBE Cholesky 34.
- ICCF : Approche incomplète - factorisation Cholesky 56.
L'approche ICCF est plus rapide que d'autres méthodes (diagonale, EBE Gauss, EBE Cholesky) et utilise approximativement le même nombre d'itérations pour obtenir la convergence, tels que les approches EBE Gauss ou EBE Cholesky. Elle n'utilise pas les opérations d'E/S du disque, mais requiert davantage de mémoire RAM. ICCF est recommandée si l'ordinateur est doté de suffisamment de RAM pour la tâche. Les exigences en termes de mémoire RAM et d'espace disque requis pour les approches EBE Gauss et EBE Cholesky sont minimes, mais ces dernières sont plus lentes que l'approche ICCF.