Il existe plusieurs types de solveurs itératifs.
FIC itérative
Cette méthode est recommandée pour les problèmes importants avec peu de côtés droits.
- Utilisation de la mémoire : importante
- Utilisation du disque : nulle
- Vitesse estimée : rapide (pour les problèmes bien conditionnés).
- Quantité d'équations : de 15 000 à 1 000 000 d'équations ou plus.
- Analyses prises en charge : les analyses statique linéaire, modale, de flambement.
- Limites d'analyse disponibles : aucunes
- Autres limitations :
- L'exactitude des restrictions structurelles n'est pas vérifiée.
- La convergence est lente si certains problèmes sont mal conditionnés.
Itérative diagonale
Cette méthode est recommandée pour les problèmes importants avec peu de côtés droits.
- Utilisation de la mémoire : minimale
- Utilisation du disque : minimale
- Vitesse estimée : lente
- Quantité d'équations : de 15 000 à 1 000 000 d'équations ou plus.
- Analyses prises en charge : les analyses statique linéaire, modale, de flambement.
- Limites d'analyse disponibles : aucunes
- Autres limitations :
- L'exactitude des restrictions structurelles n'est pas vérifiée.
- La convergence est lente si certains problèmes sont mal conditionnés.
Itérative Gauss-Cholesky
Cette méthode est recommandée pour les problèmes importants avec peu de côtés droits, lorsqu'il n'y a pas suffisamment de RAM pour utiliser la méthode ICCF.
La vérification de chaque élément de la matrice s'opère selon la procédure de régularisation Vinget 12.
- Utilisation de la mémoire : minimale
- Utilisation du disque : minimale
- Vitesse estimée : lente
- Quantité d'équations : de 15 000 à 1 000 000 d'équations ou plus.
- Analyses prises en charge : les analyses statique linéaire, modale, de flambement.
- Limites d'analyse disponibles : aucunes
- Autres limitations :
- L'exactitude des restrictions structurelles n'est pas vérifiée.
- La convergence est lente si certains problèmes sont mal conditionnés.
ICCF itérative multiniveau
Cette méthode est recommandée pour les problèmes importants avec peu de côtés droits. Elle affiche une convergence est plus rapide que la méthode ICCF itérative.
- Utilisation de la mémoire : importante
- Utilisation du disque : minimale
- Vitesse estimée : rapide (pour les problèmes bien conditionnés)
- Quantité d'équations : de 15 000 à 1 000 000 d'équations ou plus.
- Analyses prises en charge : les analyses statique linéaire, modale, de flambement.
- Limites d'analyses disponibles : types de structures disponibles : 3D (barre, coque, solide et éléments finis de type spécial), portique 2D.
- Autres limitations :
- L'exactitude des restrictions structurelles n'est pas vérifiée.
- Moins de convergence stable, dans certains cas.
Itérative diagonale multiniveau
Cette méthode est beaucoup plus lente que la méthode ICCF itérative multiniveau. Toutefois, elle requiert beaucoup moins de mémoire vive (RAM).
La méthode de lissage 2 nécessite en général moins d'itérations que la méthode ICCF itérative multiniveau.
La vérification de chaque élément de la matrice s'opère selon la procédure de régularisation Vinget 1,2.
- Utilisation de la mémoire : minimale
- Utilisation du disque : minimale
- Vitesse estimée : lente
- Quantité d'équations : de 15 000 à 1 000 000 d'équations ou plus.
- Analyses prises en charge : les analyses statique linéaire, modale, de flambement.
- Limites d'analyses disponibles : types de structures disponibles : 3D (barre, coque, solide et éléments finis de type spécial), portique 2D.
- Autres limitations :
- L'exactitude des restrictions structurelles n'est pas vérifiée.
Itérative Gauss-Cholesky multiniveau
Cette méthode est beaucoup plus lente que la méthode ICCF itérative multiniveau. Toutefois, elle requiert beaucoup moins de mémoire vive (RAM).
La méthode de lissage 2 nécessite en général moins d'itérations que la méthode ICCF itérative multiniveau.
La vérification de chaque élément de la matrice s'opère selon la procédure de régularisation Vinget 1,2.
- Utilisation de la mémoire : minimale
- Utilisation du disque : minimale
- Vitesse estimée : moyenne (pour les problèmes bien conditionnés)
- Quantité d'équations : de 15 000 à 1 000 000 d'équations ou plus.
- Analyses prises en charge : les analyses statique linéaire, modale, de flambement.
- Limites d'analyses disponibles : types de structures disponibles : 3D (barre, coque, solide et éléments finis de type spécial), portique 2D.
- Autres limitations :
- L'exactitude des restrictions structurelles n'est pas vérifiée.
Calculs de la méthode itérative
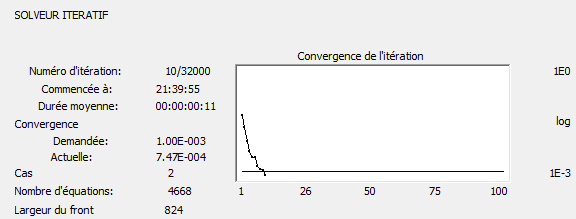
La boîte de dialogue Calculs pour la méthode itérative présente le processus de convergence de la méthode itérative si le niveau de précision défini par l'utilisateur est atteint ou si le processus est divergeant.
- Le nombre d'itérations effectuées actuelles / le nombre maximum d'itérations.
- La précision requise
- La précision de l’itération courante
- Le nombre d’équations
- La largeur avant