L'analyse temporelle est une analyse qui permet d'obtenir la réponse de la structure à une excitation imposée dans un intervalle de temps déterminé, contrairement aux autres types d'analyses disponibles qui affichent la réaction de la structure sous forme d'amplitudes obtenues à un moment unique.
L'analyse temporelle consiste à trouver la solution de l'équation de la variable de temps "t" suivante :
M * a(t) + C * v(t) + K * d(t) = F(t)
avec les valeurs initiales connues d(0)=d0 et v(0)=v0,
où :
M - matrice des masses
K - matrice de rigidité
C = a * M + b * K - matrice d'amortissement
α - coefficient multiplicateur donné par l'utilisateur.
β - coefficient multiplicateur donné par l'utilisateur.
d - vecteur de déplacement
v - vecteur de vitesse
a - vecteur d'accélération
F - vecteur de charges.
Toutes les expressions contenant le paramètre (t) dépendent du temps.
Pour résoudre l'équation présentée ci-dessus, on utilise la méthode de Newmark ou la méthode de décomposition. La méthode de Newmark fait partie du groupe d'algorithmes qui sont inconditionnellement convergents, si les paramètres de la méthode sont pris d'une façon appropriée. Elle utilise les formules suivantes pour calculer les déplacements et la vitesse à l'étape d'intégration suivante.
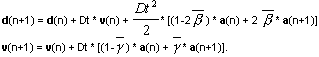
Les termes β et γ sont des paramètres de contrôle de convergence et de précision de la méthode.
La convergence inconditionnelle est assurée lorsque 0,5 ≤ γ 2 ≤ * b.
Les valeurs b = 0.25 et g = 0.5 sont adoptées. Il est possible de changer ces valeurs, mais uniquement en cas d’utilisation de l’analyse temporelle linéaire, si la méthode de Newmark ou la méthode de Newmark (accélération) est utilisée. La modification de ces valeurs (paramètres TransBêta et TransGamma) est possible dans le fichier de préférences *.COV enregistré dans le répertoire CFGUSR. Pour effectuer les calculs pour d’autres valeurs des paramètres b et g, il faut modifier ces paramètres TransBêta et TransGamma dans le fichier *.COV, et ensuite charger ce fichier de préférences.
La méthode de Newmark est conseillée dans le cas d'instants courts, quand la structure est sollicitée par les charges concentrées. De telles charges entraînent un mouvement qui exigera une quantité importante de modes propres à décrire. De ce fait, la méthode de Newmark sera plus efficace que la méthode de décomposition modale pour ce type de tâche. La méthode de Newmark utilise les équations d'analyse temporelle de base sans effectuer aucune simplification. La précision de la résolution obtenue dépend de la précision d'intégration numérique de l'analyse temporelle, et pour les paramètres sélectionnés α, β, elle est définie par la valeur de l'intervalle de temps. Cette méthode n'exige pas la résolution du problème propre pour déterminer les valeurs et les vecteurs propres. Pour les instants longs, cette méthode demande trop de temps parce qu'il faut effectuer les calculs pour une grande quantité de pas temporels avec la précision demandée.
La méthode Hliber-Hughes-Taylor (HHT) permet d’introduire un amortissement numérique de fréquences supérieures sans perdre la précision de la solution. La forme discrète de l’analyse temporelle prend l’aspect suivant :
où :
-1/3 ≤ α ≤ 0
Si l’on admet ce qui suit :
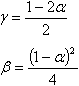
On obtient un schéma d’intégration inconditionnellement stable avec une précision de second ordre.
Pour le mode d’accélération, les grandeurs ‘d’essai’ dans le pas n+1 de l’intégration sont déterminées de la manière suivante.
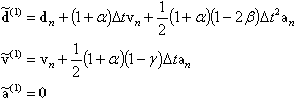
La méthode HHT est un algorithme efficace pour l’intégration numérique, car il permet d’éliminer l'impact défavorable de hautes fréquences sur la qualité de la solution.
Une méthode simple pour obtenir la résolution est la méthode de décomposition modale, basée sur la représentation du mouvement de la structure en tant que superposition du mouvement pour les formes non conjuguées. De ce fait, cette méthode demande de déterminer les valeurs et les vecteurs propres. A cette fin, il est conseillé d'utiliser la méthode de Lanczos, suivie de la vérification de Sturm. La méthode de décomposition modale utilise les équations réduites non conjuguées.
L'analyse temporelle (sans amortissement) peut être exprimée par la formule suivante :
où :
![]() ,
,
Où Ng - nombre de "groupe de charge", φk(t) - historique de temps pour le k-ème groupe de charge.
![]() (2)
(2)
A la suite de l'insertion de l'équation (2) dans l'équation (1) et après la prise en compte de l'amortissement modal et des conditions d'orthogonalité ![]() , on obtient l'équation suivante :
, on obtient l'équation suivante :
où ![]() , ξ - paramètres de l'amortissement modal, ωi - fréquence pour le i-ème mode.
, ξ - paramètres de l'amortissement modal, ωi - fréquence pour le i-ème mode.
Chacune des équations d'analyse temporelle est résolue de façon numérique avec une approximation de deuxième ordre. Le vecteur de déplacement X(t) pour les points de temps t* = t1, t2... est obtenu après l'introduction de qi(t*), i=1,2, …, m dans les équations (2).
Il convient d'observer les différences entre les types d'analyse disponibles décrits dans ce chapitre. La différence entre l'analyse des charges roulantes et l'analyse temporelle réside dans le fait que le premier type ne prend pas en compte les effets dynamiques. La différence entre l'analyse harmonique et l'analyse temporelle réside dans le fait que le premier type d'analyse indique la réponse de la structure uniquement sous forme d'amplitudes, et non en fonction du temps.
Rubrique connexe :