A generalized eigenvalue problem is defined in the following manner:
K φ - λM φ = 0,
where K, M denote stiffness and mass matrices respectively, {φ, λ} - eigenpairs (natural vibration mode and eigenvalue).
Two types of residual vectors are defined:

where {φ, λ} designate calculated eigenpairs which include certain calculation errors. The first expression defines a residual vector in terms of forces, whereas the second one defines terms of displacements.
Three different criteria of estimating calculation errors for eigenvectors are applied:

Methods
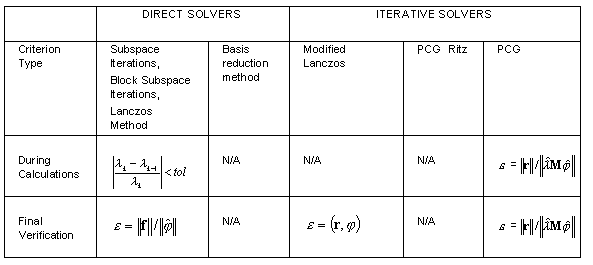
Comments
- Precision during structure calculations for the Lanczos and modified Lanczos methods (iterative solver) for pseudo mode is not determined. Only final verification is performed.
- Convergence check
 at each of the 20 Lanczos steps for seismic mode is conducted. The tol parameter in the Modal Analysis Parameters dialog is ignored.
at each of the 20 Lanczos steps for seismic mode is conducted. The tol parameter in the Modal Analysis Parameters dialog is ignored. - Basis reduction and PCG_Ritz are the Ritz methods. Precision verification is not performed. The tol parameter in the Modal Analysis Parameters dialog is ignored.
- PCG for iterative solver applies the most stiff convergence criteria
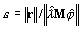 during calculation. The tol Parameter in the Modal Analysis Parameters - Iterative Solver dialog defines the top bound for ε, thus ε ≤ tol is a condition for stopping iterations.
during calculation. The tol Parameter in the Modal Analysis Parameters - Iterative Solver dialog defines the top bound for ε, thus ε ≤ tol is a condition for stopping iterations.
Precision should not be confused with the tolerance determined in the Modal Analysis Parameters dialog while using skyline or sparse direct solvers, if modal mode is selected. Tolerance during calculations is defined according to the following formula.

where λk, λk-1 - two successive eigenvalues on k, k-1 iteration steps and tol denotes the tolerance, adopted in the Modal Analysis Parameters dialog . Determining the final accuracy of calculations (1-3) is time-consuming and performed at the final stage of modal analysis to verify obtained precision. Decrease tol tolerance to increase calculation accuracy which increases the iteration number.
If precision of some modes after calculations is insufficient, the following is necessary.
|
DIRECT SOLVERS |
ITERATIVE SOLVERS |
|||
|---|---|---|---|---|
|
Subspace iterations, block subspace iterations, Lanczos method |
Basis reduction method |
Modified Lanczos |
PCG_Ritz |
PCG |
|
Decrease tol in the Modal Analysis Parameters dialog |
Increase number of basis nodes and basis directions |
Decrease the tol in Iterative Solver Parameters dialog and increase the number of modes |
Increase the number of modes |
Decrease the tol value in Modal Analysis Parameters dialog |
See also: