During calculations of an orthotropic slab, an eqivalent stiffness on a section level is calculated at each point. For a 2D shell element in 3D, stiffness is determined on the basis of the following matrices:
- membrane stiffness matrix D
- bending stiffness matrix K
- shear stiffness matrix H.
Assuming that orthotropy is defined only for 2D elements and that the section is symmetrical, it is not necessary to determine the matrices that combine flexural and membrane states.
The sections of double-sided unidirectional ribs, unidirectional box floors, bi-directional box floors, and grillage constitute symmetrical sections and the above approach is fully justified. However, for the remaining types the above approach produces only an approximation.
The reference plane for defining stiffness should be adopted at the level of the center of gravity rather than as a middle line (plate thickness). It is a more correct approach, particularly taking transversal vibrations into account. However, it is also an approximation when calculating stiffness, but it is better than adopting thickness as a middle line.
The slab stiffness is determined on the basis of the following matrices:
- bending stiffness matrix K
- shear stiffness matrix H.
The stiffness values that refer to the orthotropy directions are given by the matrices assuming the general form:
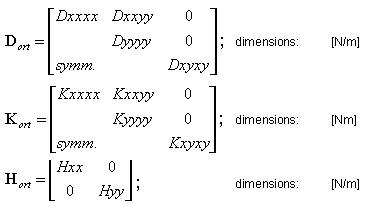
The X orthotropy direction is user-defined (a direction vector definition) just as when you define the local system for result or reinforcement presentation V =[vx,vy,vz].
The rule used to determine how the user-defined vector V generates the direction of the orthotropy system X axis:
"The X direction is the direction tangential to the element plane that is the closest to the defined V direction."
If {e 1 ;e 2 ;e 3 } constitute a local base in the given element point (for plates in 2D, e i coincides with the directions of global axes XG, YG), then the trigonometric functions sin α ; cos α of the a angle included between the orthotropy X direction and the local x1 axis are defined as:

After the trigonometric functions s = sin α ; c = cos α of a angle are determined, the stiffness matrices are transformed from the XY orthotropy axis system to the local directions on an element, taking advantage of the following formulas:
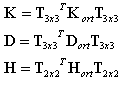
where:
T3x3 is the transformation matrix for the 2 order tensor in 2D (presented as the 3x3 matrix)
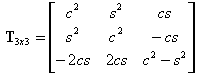
T2x2 is the matrix presenting transformation of 2D vector

See also: