Os cálculos são semelhantes aos cálculos de uma viga retangular e incluem a avaliação das forças em uma viga e nos nós de um painel (laje). Em seguida, as forças são reduzidas para o centro de gravidade de uma nova seção T.
O eixo passa através do centro de gravidade do painel.
Para calcular as forças de um painel, multiplique as forças nos nós do painel (nós comuns do painel e da viga) pela largura efetiva da laje (abordagem simplificada). Ao posicionar a viga em relação à laje, os deslocamentos são considerados (inclusive os deslocamentos relativos). No exemplo a seguir, os resultados de redução obtidos de uma seção T foram deslocados do plano do painel pelo deslocamento que equivale à distância do centro de gravidade do painel e do centro de gravidade da seção T.
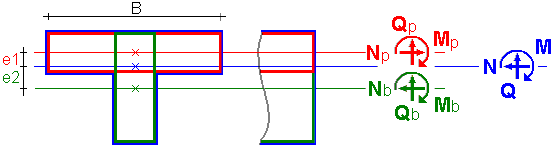
A redução das forças para o centro de gravidade da seção T é a seguinte:
M = Mb + Mp * B + Np * B * e1 + Nb * e2
Q = Qb + Qp * B
N = Nb + Np * B
em que:
B = beff1+b+beff2
Definição do centro de gravidade de uma seção T
Um momento estático calculado no centro de gravidade do painel (uma viga e seu deslocamento somente são manipulados)
S = b*h*(deslocamento)
A = (beff1+b+beff2)*hpl + b*h
O centro de gravidade foi deslocado em relação ao centro de gravidade do painel:
Z = S / A
em que:
b – largura da viga
h – altura da viga
beff1, beff2 – larguras efetivas da laje
hpl – altura da laje (espessura do painel)
deslocamento – deslocamento da viga em relação ao painel
NOTAS:
- É importante observar que podem existir partes comuns da área do painel e da viga; infelizmente, elas são contadas duas vezes nos cálculos, o que provoca o aumento da rigidez da viga T. Em consequência, as forças e as deflexões são menores.
- Os resultados do painel são lidos nos nós dos elementos finitos; o refinamento da malha tem efeito nos resultados.
- No modelo, o eixo da seção T é o eixo do centro de gravidade do painel.
- A multiplicação das forças relevantes no painel pela largura da laje efetiva constitui uma simplificação. Em consequência, os resultados são aproximados.