O algoritmo para deflexões de lajes de CA é baseado no uso de cálculos de uma laje elástica isotrópica feita de um material elástico. As alterações de rigidez do material devido à fissura são consideradas. Os deslocamentos são calculados aplicando o Método de elementos finitos (FEM) e, em seguida, são modificados.
Os cálculos são executados separadamente para cada painel. Tal suposição estará correta se um painel puder ser identificado com um elemento estrutural (vão, segmento de piso); caso contrário, os valores de rigidez em média em um painel poderão ser distorcidos. Isso pode resultar na influência de elementos muito distantes nos deslocamentos de um FE analisado. A influência de tais distúrbios em valores extremos não é muito significativa; no entanto, os mapas de deformação (deflexão) devem ser tratados com muito cuidado.
É recomendável modelar cada segmento de piso em que extremos locais de deflexões podem ocorrer como um painel separado. Esse painel deve ser definido dentro dos limites definidos pelos suportes em torno dele (de forma semelhante aos vãos que são limitados por suportes no caso de vigas). Para um painel, esses suportes não precisam ser contínuos em todo o contorno do painel.
A divisão em painéis não afeta os resultados da verificação usando o método Com atualização de rigidez (FEM), contanto que as cargas, a geometria e a armadura calculada sejam as mesmas.
Os cálculos são executados para uma combinação selecionada (separada para os deslocamentos inferior e superior) ou um grupo de combinações, se isso for exigido pela norma (combinações frequentes, raras e quase permanentes). Essa combinação é escolhida para cálculos para os quais há deslocamentos elásticos máximos (positivos e negativos separadamente). Se um painel não puder ser tratado como um elemento estrutural (ele compreende mais elementos de estrutura), os mapas de deformação (deflexão) deverão ser tratados com muito cuidado. No entanto, não tem influência significativa nos valores de deflexão extremos para um determinado painel.
Deve-se prestar atenção aos deslocamentos dos cantos restantes suportados de uma laje.
O algoritmo de cálculo usado no programa Robot é baseado na suposição de que as deflexões (reais) totais de uma laje de CA é igual ao produto de suas deflexões elásticas e o coeficiente de rigidez D/B.
em que:
– Deslocamentos reais do ponto de cálculo de ordem i de uma laje que levam em conta a fissura e a armadura calculada
– Deslocamentos elásticos do ponto de cálculo de ordem i de uma laje
D – Rigidez da laje assumindo elasticidade do material (como nos cálculos FEM)
B – Rigidez equivalente de uma laje de CA, calculado considerando a fissura do elemento, os efeitos reológicos, a aderência da armadura calculada etc. e a média calculada para ambas as direções.
Tal abordagem se resume ao dimensionamento linear de deslocamentos elásticos individuais pelo coeficiente global de redução da rigidez.
O algoritmo de cálculo para o método de rigidez (elástico) equivalente é o seguinte:
Após executar a análise da estrutura usando o FEM e calcular a área de armadura necessária para o estado limite máximo, o estado limite do grau do serviço (no que diz respeito aos cálculos de fissuras, limites de tensão ou outros problemas que podem ser considerados localmente) e o estado limite acidental, a rigidez para cada elemento finito (FE) será avaliada no programa. Os cálculos de rigidez são executados para duas direções de armadura. O escopo e o método de cálculo desses valores de rigidez dependem dos requisitos detalhados de um determinada norma. Como resultado desses cálculos, dois valores de rigidez (diferentes na maioria dos casos) são obtidos para cada elemento finito. Para cálculos adicionais, é usada uma média ponderada dos valores de rigidez do componente. O peso da média é a relação de momentos que atuam em um determinado elemento em ambas as direções.
em que:
Bx, By – Valores reais de rigidez calculados para duas direções de armadura
cf – Coeficiente de peso calculado de acordo com a fórmula.
- Se | Mxx | / | Myy | > 4, então cf = 1
- Se 0,25 ≤ | Mxx | / | Myy | ≤ 4, então
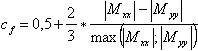
- Se | Mxx | / | Myy | < 0.25, então cf = 0.
Como resultado da aplicação dessas fórmulas, no caso de grandes desproporções de momentos (a relação entre o momento maior e o menor é maior ou igual a 4,0), é considerada a rigidez da direção de ação do maior dos momentos. Quando os valores de momentos são similares, a espessura de uma determinada direção é atribuída proporcionalmente à relação de momento.
A próxima etapa é avaliar a relação da rigidez elástica com a média ponderada dos valores de rigidez real obtidos como mencionado acima. Esse cálculo é executado para cada elemento finito.
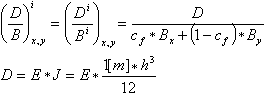
O coeficiente de laje (1 – n*n) é considerado nos cálculos de rigidez B e D.
Os valores reais de rigidez obtidos nos cálculos podem ser visualizados ao ativar os mapas de Fator de rigidez.
Se as propriedades dos materiais usados durante o projeto forem idênticas às usadas em um modelo, o valor do coeficiente D/B > 1,.0. Esse coeficiente pode ser interpretado (principalmente para lajes sujeitas a flexão unidirecional) como um multiplicador de deflexão elástica. Se diferentes materiais forem usados em um modelo e cálculos (por exemplo, com diferentes classes, como concretos com diferente módulo de Young ou coeficiente de Poisson), o valor do coeficiente será corrigido automaticamente. Isso pode resultar na interrupção da desigualdade mencionada anteriormente.
A etapa a seguir é calcular a média das relações de rigidez avaliadas anteriormente. A relação de rigidez global final, usada para o cálculo de deslocamentos reais de uma laje (como escala linear de deslocamentos elásticos) é uma média das relações de rigidez (com o peso igual a 0,25) e a relação de rigidez registrada para um elemento no qual há um extremo do momento de flexão atuando em qualquer direção (com o peso igual a 0,75).
O algoritmo do método de rigidez equivalente (elástico) assume a média da rigidez para todos os elementos finitos; uma forma da linha de deflexão é, portanto, idêntica à linha de deflexão multiplicada pelo coeficiente de rigidez.
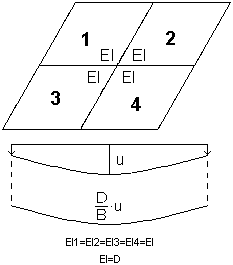
O algoritmo do método com atualização de rigidez (inelástica) é idêntico ao algoritmo do método de rigidez equivalente (elástico) até que a rigidez calculada seja atribuída independentemente a cada elemento finito (rigidez diferente para a direção X e a direção Y). Uma laje anisotrópica de vários valores de rigidez é obtida. Para os valores de rigidez assim determinados, a deflexão da laje é calculada.
No método com atualização de rigidez, a rigidez de cada elemento é calculada de forma independente, portanto, as linhas de deflexão podem ser diferentes. Uma rigidez diferente é obtida para cada elemento finito para cada direção.
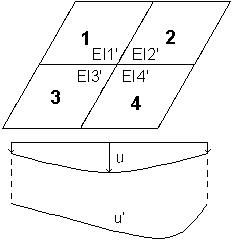
Se a opção de correção da armadura estiver selecionada na guia Parâmetros SLS na caixa de diálogo Parâmetros de armadura de placa e casca durante os cálculos, a área da armadura aumentará (para aumentar a rigidez do elemento), o que reduz as deflexões da laje.
A armadura em ambas as direções é distribuída na proporção inversa da rigidez. Quando não for possível limitar as deflexões abaixo do valor de deflexão admissível definido pelo usuário (quando não for possível executar uma correção adicional da armadura devido à taxa de armadura permitida), quando os cálculos da área de armadura necessária forem concluídos, um aviso informará que o valor de deflexão admissível foi excedido para o painel.
Não há limites predefinidos na armadura que não sejam aqueles em normas. Observe o aspecto econômico da solução fornecida e, que quanto mais uma deflexão difere dos requisitos, menos eficaz é o método usado.