As estruturas de cabo são estruturas com cabos como elementos principais de carga. Se uma das principais cotas de um elemento for maior do que as duas restantes e a rigidez da seção em relação à flexão e à torção for pequena em comparação com a rigidez da tensão, tal elemento será considerado um cabo.
A conclusão básica obtida com base na definição anterior é que somente as forças de tração podem ser aplicadas aos cabos. No entanto, em alguns casos, podem ser aplicados aos cabos pequenos momentos fletores ou de torção e forças de cisalhamento. A vantagem mais significativa de usar estruturas de cabos é o fato de que os cabos têm grandes tensões de tração admissíveis.
Portanto, é possível usar uma seção de cabo de forma que seja possível projetar estruturas leves, econômicas e estéticas. Existem duas vantagens em usar elementos de cabo em estruturas projetadas:
- Inserir a tensão inicial do cabo regula a força interna e torna os resultados mais eficazes.
- Montagem simples (como suspensão e montagem de toda uma estrutura, por causa de seu peso mais leve).
A teoria das estruturas de cabos é baseada nas seguintes suposições:
- As cargas e outros efeitos externos são de tipo quase estático e constantes no tempo
- Nos cabos, não são considerados os momentos fletores nem as forças de cisalhamento
- Os elementos de cabo funcionam na faixa elástica (módulo de Young E = const)
- Qualquer carga pode ser aplicada, exceto cargas de momento
- Deslocamentos grandes u, mas gradientes pequenos du/dx são permitidos
- A área F da seção do cabo é constante (F=const)
- Comprimento do cabo sem carga = l
Equações que regem o problema
Consideremos um pequeno cabo côncavo (ou seja, um cabo para o qual o ângulo entre a tangente em qualquer ponto do cabo e uma linha reta que une suas extremidades é pequeno), carregado com uma carga arbitrária em seu plano. Consideremos um elemento infinitesimal nesse cabo, que é descrito no estágio inicial (primeiro, estágio de montagem) pela carga q0, temperatura T0 e tensão H0; o comprimento desse elemento é igual a dso (Fig. 1a). Após a carga ter sido aplicada ao cabo (segundo, estágio final com a carga q, temperatura T e tensão H), o comprimento de uma seção de cabo elementar é igual a ds (Fig. 1b). Ambos os estágios, juntamente com as cargas em ambos os planos (xy e xz), também são exibidos na Fig. 2.
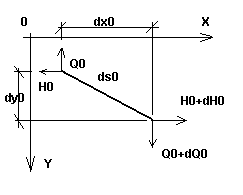 Fig. 1a |
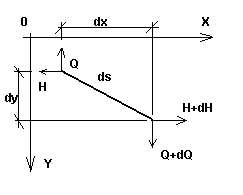 Fig. 1b |
Considerando um valor pequeno de concavidade do cabo e levando em conta que a força total do cabo deve ser tangente ao cabo, é possível atribuir o alongamento apropriado do cabo como uma função somente de valores estáticos. Após a integração ao longo do comprimento total do cabo, é obtida a fórmula conhecida para um cabo com um valor pequeno de concavidade do cabo. O valor D de alongamento do banzo do cabo pode ser derivado de (1).
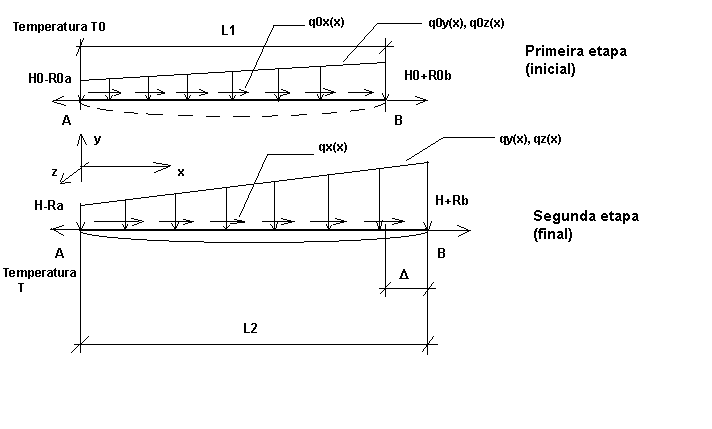
Fig. 2
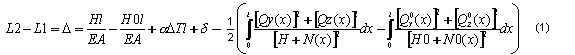
em que:
A, B – Nó de cabo inicial e final
EF – rigidez da tensão do cabo (em que: E – módulo de Young, F – área de seção transversal do cabo)
a – Coeficiente da expansão térmica
l – Comprimento inicial do cabo (para cabo sem carga)
D – Alteração de distância entre os apoios
d – Encurtamento/alongamento interno inicial do cabo (regulamento)
DT – Alteração da temperatura
Q(x) – Função da força de cisalhamento para uma viga com apoios rotulados (de acordo com os índices: respectivamente nas direções do eixo Y e do eixo Z e para os estágios inicial e final). Consulte Fig. 3a.
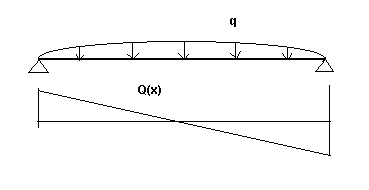
Fig. 3a
N(x) – Função da força axial causada pela carga estática para uma viga com apoios fixos (durante o estágio inicial ou final). Consulte Fig. 3b.
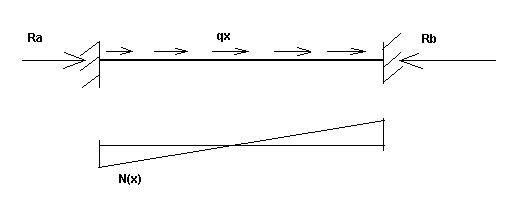
Fig. 3b
Também é possível observar que na equação do cabo (1), ao contrário das soluções tradicionais aplicadas aos cálculos de cabos, a força axial pode variar ao longo do comprimento do cabo (em denominadores de ambas as funções de integração na equação (1), os seguintes componentes funcionais existem: [H+N(x)] 2 e [H0+N0(x)] 2 ). Isso permite resultados mais precisos.
Consulte também: