Comentários introdutórios:
As cargas, na sua grande maioria, se originam na gravidade (massa). Portanto, o cálculo dinâmico precisa que essas massas sejam levadas em conta. Para permitir que o usuário converta com facilidade cargas estáticas (cargas de gravidade) em massas, o comando especial “MASses ACTive” foi aplicado no analisador de arquivos de texto.
Isso permitirá que os usuários definam a carga somente uma vez para fins de análise estática e, em seguida, a use para criar a distribuição de massa no modelo computacional da estrutura para executar qualquer análise dinâmica.
O comando precisa de dois elementos para uma conversão bem-sucedida. O primeiro é o conjunto de direções em que as massas estarão ativas. Normalmente, todas as direções globais (X, Y, Z) são usadas, porque somente em cálculos específicos a inércia não age em todos eles. O segundo é a magnitude da inércia. Isso é definido pelo número do caso de carga estática e a direção das cargas, que são levados em conta durante a conversão. Além disso, um coeficiente extra pode ser fornecido para multiplicar o valor da carga.
O caráter da carga é automaticamente transformado em massas: forças concentradas são transformadas em massas concentradas; momentos em inércia rotacional; forças distribuídas em massas contínuas.
Sintaxe:
ANA [ DYN | MOD | TRAN | HAR | SEIsmic | SPEctral ],(diz respeito a todos os tipos de análise dinâmica)
CASe (#<number> <name>)
MASess ACTive [X/Y/Z]
[X|Y|Z ] (MINus|PLus) <case_list> COEfficient=<c>
Princípios gerais:
r = r(x) é uma função da distribuição de densidade de massa dentro de um determinado elemento enquanto N(x) é a matriz de função de interpolação nodal (matriz de função de forma). Como base de tratamento adicional, uma matriz de massa consistente de um elemento será criada de acordo com a seguinte fórmula geral (1):
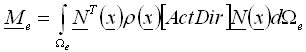 , (1)
, (1)
em que:

Os sinalizadores de atividade de direção global são definidos por MASess ACTive [X/Y/Z], ou seja, qualquer direção estará ativa, se especificada. Essa é a consequência do estilo do tratamento de massa geral do Robot, em que alguns componentes de forças de inércia podem ser ignorados durante a análise.
A matriz de massa será criada com base em todas as cargas que pertencem a todos os casos de carga especificados em <case_list> que atuam no elemento/nó atual, de acordo com as seguintes regras:
- Cada registro de carga de um caso especificado é convertido em massa separada e independentemente de outras cargas e massas.
- Somente casos de carga simples (sem combinações !) podem aparecer na lista (mas, em um caso dinâmico, a lista de casos estáticos pode ser fornecida para ser convertida em massas).
- A matriz de massa total é criada como uma soma das matrizes de massa de todos os componentes de carga acima e da massa predefinida em virtude do peso morto da estrutura e/ou das massas de elementos especificadas. Portanto, também será enviada parte de uma matriz de massa originada de cargas para diagonalização e/ou negligência da parte de inércia rotacional, se especificado pela configuração COH|CON, ROT.
- O valor da função de densidade em um determinado ponto é criado como o valor da projeção do vetor de força atual f no vetor n de direção global exclusiva e obrigatoriamente especificada
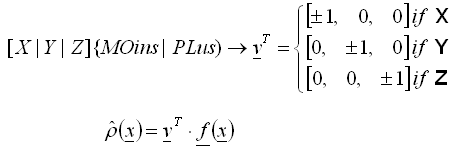 , (2)
, (2) - Somente valores positivos são levados em conta em cada ponto de integração, portanto
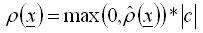 , (3) Nota: As regras acima pretendem permitir uma seleção fácil de cargas originadas da gravidade. Como não existe nada parecido com a direção de gravidade padrão, a especificação de direção assinalada deve ser feita pelo usuário.
, (3) Nota: As regras acima pretendem permitir uma seleção fácil de cargas originadas da gravidade. Como não existe nada parecido com a direção de gravidade padrão, a especificação de direção assinalada deve ser feita pelo usuário. - Todas as direções usadas para definir a conversão de carga em massa devem ser aceitáveis para o tipo de estrutura geral atual, portanto, PLAte aceita somente a direção Z, para outros tipos de plano somente X e Y serão aceitos. As especificações de direção incompatíveis serão ignoradas ou será exibido um erro. Os tipos estruturais 3D aceitam todas as direções globais.
Exemplo:
Considere uma viga, carregada centralmente pela carga de gravidade Fy= - 120 kN. Suponha que o caso estático mostrado abaixo tenha um número 3. Para calcular os modos de vibração livre dessa estrutura no caso número 10, levando em conta esta massa (Fx=Fy= 12.232 kg), é possível usar o seguinte comando:
ANA MOD=3 MAS=CON
CAS #10 modal
MASses ACTive X Y
Y MINus 3

Detalhes da conversão para diferentes tipos de carga
Cargas que atuam em elementos de viga
- carga uniforme do elemento
[Px=<px.>/Py=<py>/Pz=<pz>] (LOCal/GLObal) (PROjected) ([R=<r>])([R=<r>])
O vetor de densidade da carga é transformado em direções globais como especificado pela configuração:
(LOCal/GLObal) (PROjected) ([R=<r>]), levando em conta o sinalizador (PROjected) para o tratamento de carga, e a distribuição de massa uniforme é definida de acordo com (2) (3)
- carga morta
A carga morta é convertida em massa equivalente à carga uniforme do elemento
Nota: Essa operação deve ser usada com cautela, pois a massa originada da carga morta da estrutura é considerada automaticamente em cálculos dinâmicos (se apenas a densidade do material for maior que 0) - carga do elemento variável
(X=<x1>)[ P=<p1>] ((JUSque)(X =<x2>)[P=<p2>] ) (R=<r>) (LOCal/GLObal) (RELative) (PROjected)
a carga é transformada em direções globais conforme especificado pela configuração:
(LOCal/GLObal) (PROjected) ([R=<r>])
e a distribuição de massa uniforme é definida de acordo com (2)(3)
Nota: A regra (3) implica o tratamento a seguir de carga de sinal variável, para cada registro de carga (componente) separadamente (não para a carga total, que é a soma de todas as cargas que atuam em um determinado elemento), como mostrado na Fig. 1.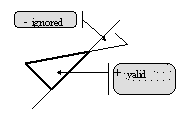 Fig. 1
Fig. 1 - força do elemento concentrado
[X=<x>] [F=<f>](R=<r>) (Local)(RELative)
A massa total m concentrada em um ponto x 0 é avaliada com base na representação global do vetor de força f da seguinte maneira:
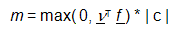 , (4)
, (4) Em seguida, a matriz de massa consistente é avaliada, como se a distribuição de massa fosse representada pela função delta de Dirac, levando a:
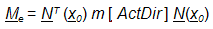 , (5)
, (5) - momento do elemento concentrado
[X=<x>] [F=<fc>] (R=<r>) (LOCal)(RELative)
Como a especificação de direção de massa não diz respeito às direções de inércia rotacional, uma regra separada deve ser estabelecida para executar a conversão entre o momento de elemento concentrado e a inércia rotacional de um determinado corpo anexado ao elemento.
A transformação do estilo de vetor de <fc> é executada de acordo com as configurações (R=<r>) (LOCal) para obter um vetor I referenciado para o sistema de coordenadas local do elemento. Para omitir a necessidade de transformação de estilo de vetor inconsistente (enquanto um tensorial deve ser usado), a carga deve ser fornecida como LOCal e nenhum R=<r>. Caso contrário, será exibido um aviso
Assume-se que as coordenadas locais do elemento coincidam com o eixo principal de inércia do corpo, portanto,
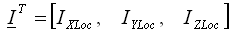 representa os momentos de inércia principais nas coordenadas locais do elemento. Com base nisso, resulta a seguinte limitação de modelagem:
representa os momentos de inércia principais nas coordenadas locais do elemento. Com base nisso, resulta a seguinte limitação de modelagem: 
Fig. 2
Situação correta
Situação incorreta, modelagem impossível
- momento de elemento distribuído
[M=<m>] (LOCal)
Nessa definição, <m> é um vetor que, após a transformação do estilo de vetor para o sistema de coordenadas local do elemento, representa as densidades de inércia rotacional referenciadas para o eixo local do elemento por comprimento do elemento.
Aplicam-se todas as noções no que se refere ao momento de elemento concentrado (veja a Fig. 2).
Cargas que atuam em elementos de superfície
- carga uniforme do elemento
[Px=<px.>/Py=<py>/Pz=<pz>]
O vetor de densidade da carga é avaliado e, em seguida, transformado em densidade de massa de acordo com (2)(3)
- carga morta
A carga morta é convertida em carga uniforme equivalente e tratamento adicional como acima
Nota: Essa operação deve ser usada com cautela, pois a massa originada da carga morta da estrutura é considerada automaticamente em cálculos dinâmicos (se apenas a densidade do material for maior que 0) - carga do elemento variável
[P=<p1>] AU <n1>( [P=<p2>AU<n2> ([P=<p3> AU<n3>))
Em cada ponto de integração, a densidade de carga é avaliada e, em seguida, transformada em densidade de massa de acordo com (2)(3), veja a Fig. (1). As regras de integração aprimoradas são usadas com
NGAUS = 3x3 para Q8,
= 7 para T6,
= 2x2 para Q4
= 3 para T3
- carga variável dentro de um contorno
[P=<p1>] AU <n1>( [P=<p2>AU<n2> ([P=<p3> AU<n3>)) PROjected DIRection <v> _CONtour <l_node>
Em cada ponto de integração, a densidade de carga é avaliada e, em seguida, transformada em densidade de massa de acordo com (2)(3), veja a Fig. (1). No caso em que nem toda a área do elemento pertence ao contorno, a integração totalmente automática na malha de até 100x100 pontos é executada dentro do elemento, para alcançar a precisão necessária. Portanto, o uso dessa opção pode, às vezes, tornar mais lento o processo de avaliação da matriz de massa.
- carga variável ao longo da linha
LIN
<n1>[P=<p1>] Jusque <n2> (P=<p2>) ( [LOCal (GAMma=<gamma>)] )
Somente a força de translação pode ser convertida na massa do elemento distribuída ao longo da linha.
A regra de integração do tipo Gauss de 3 pontos é usada em cada segmento da linha que cruza o elemento. Em cada integração, o vetor de densidade de carga é transformado em sistema de coordenadas global e, em seguida, tratado de acordo com (2)(3) para avaliar a distribuição de massa ao longo da linha.
- carga concentrada no ponto auxiliar
NODe (auxiliar)
F=<f> ( [R=<r>] )
Somente a força de translação pode ser convertida na massa do elemento (para o momento dos elementos da viga – a conversão da inércia rotacional foi permitida, aqui é proibida). O vetor de força <f> é transformado, se necessário, para o sistema de coordenadas global e, em seguida, tratado de acordo com (2), (3) para avaliar o valor de massa anexado ao ponto dentro do elemento, depois a matriz de massa é avaliada usando (5). O elemento ao qual a massa será anexada é pesquisado automaticamente.
Cargas nodais
- força concentrada
NODe
F=<f> ( [R=<r>] )
Vetor de força <f> tratado de acordo com (2)(3) para avaliar o valor da massa nodal
- momento concentrado
NODe
F=<c> ( [R=<r>] )
Como a especificação de direção de massa não diz respeito às direções de inércia rotacional, uma regra separada deve ser estabelecida para executar a conversão entre o momento nodal concentrado e a inércia rotacional de um determinado corpo anexado ao nó.
A transformação do estilo de vetor de <fc> é executada de acordo com a configuração (R=<r>) para obter um vetor
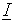 referenciado ao sistema de coordenadas global. Para omitir a necessidade de transformação de estilo de vetor inconsistente (enquanto um tensorial deve ser usado), nenhum LOCal deve ser fornecido e nenhum R=<r>. Caso contrário, será exibido um aviso.
referenciado ao sistema de coordenadas global. Para omitir a necessidade de transformação de estilo de vetor inconsistente (enquanto um tensorial deve ser usado), nenhum LOCal deve ser fornecido e nenhum R=<r>. Caso contrário, será exibido um aviso. Assume-se que as coordenadas globais coincidem com o eixo principal de inércia do corpo, portanto
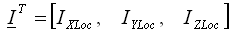 representa os momentos de inércia principais nas coordenadas locais globais. Nota: Essa regra é diferente das usadas no caso de massa concentrada anexada ao elemento de viga.
representa os momentos de inércia principais nas coordenadas locais globais. Nota: Essa regra é diferente das usadas no caso de massa concentrada anexada ao elemento de viga.