Effektive Spannungs- und Dehnungsmessungen für die Voraussage der Schädigungsentwicklung
Verwenden Sie die durchschnittlichen Spannungszustände der Konstituenten, um unabhängig den Schädigungsbeginn zu identifizieren.
Im energiebasierten Materialdegradationsschema verwendet Helius PFA die durchschnittlichen Spannungszustände der Konstituenten, um in den Matrix- und den Faserkonstituenten unabhängig den Schädigungsbeginn zu identifizieren. Die Kriterien für den Schädigungsbeginn in der Matrix und den Fasern entsprechen den einzelnen Ausfallkriterien für Konstituenten, die oben beschrieben wurden (Ausfallkriterium für Matrixkonstituenten und Ausfallkriterium für Faserkonstituenten). Sobald eine Schädigung in der Matrix- oder Faserkonstituente eintritt, beginnt die Skalar-Schädigungsvariable (D m für Matrix oder D f für Faser) sich von null in Eins-Element zu entwickeln. Die Schädigungsvariablen (D m und D f ) dienen als Steifheitsreduktionfaktoren für die verschiedenen Verbundmodule wie unten gezeigt.
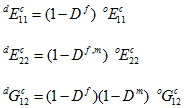
In den Ausdrücken für die beschädigten Verbundmodule oben gibt der vorangestellte Exponent d an, dass die Mengen degradiert (oder beschädigt) sind, während der vorangestellte Exponent o die ursprünglichen (nicht beschädigten) Mengen anzeigt. In den oben genannten Gleichungen steht Df,m für Dm, wenn Dm > 0, andernfalls steht Df,m für Df.
Beachten Sie, dass das beschädigte Schermodul sowohl von Dm als auch von Df abhängig ist. Dies zwingt den Schermodul, nichtlinear zu degradieren, wenn beide Konstituenten fehlgeschlagen sind. Es erzwingt eine streng abnehmende Funktion für die Degradation, die sicherstellt, dass die verbrauchte Energie immer positiv ist.
Sobald für ein oder beide Konstituentenmaterialien ein Schaden eintritt, ist ein Ausdruck für die Entwicklung des Konstituentenschadens erforderlich, der für jeden Dehnungszustand des Materials verwendet werden kann. Hierfür ist zu empfehlen, ein effektives Skalarmaß für Spannung und Dehnung zu verwenden, das für jede Konstituente (Faser und Matrix) geeignet ist. Für die Voraussage der Schädigungsentwicklung innerhalb der Matrixkonstituente definieren wir eine effektive Spannung und Dehnung wie folgt.
Effektive Spannung für die Matrix: 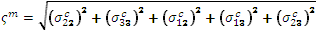
Effektive Dehnung für die Matrix: 
Für die Voraussage der Schädigungsentwicklung innerhalb der Faserkonstituente definieren wir eine effektive Spannung und Dehnung wie folgt.
Effektive Spannung für die Faser: 
Effektive Dehnung für die Faser: 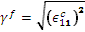
Es sollte betont werden, dass diese effektiven Matrix- und Faserwerte direkt aus den zusammengesetzten mittleren Spannungs- und Dehnungskomponenten errechnet werden, ohne auf die MCT-Zerlegung zurückgreifen zu müssen.
Die Entwicklung der Konstituentenschädigungsvariablen wird bezogen auf diese effektiven Dehnungen wie unten dargestellt ausgedrückt.
Df ist die Faserschädigungsvariable (0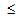 Df
Df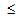 1) und wird berechnet durch
1) und wird berechnet durch
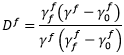
Dabei ist 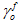 der Wert von
der Wert von 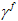 bei Schädigungsbeginn und
bei Schädigungsbeginn und 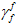 ist der Wert
ist der Wert 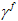 , wenn das Material vollständig zerfällt (Steifheit null erreicht).
, wenn das Material vollständig zerfällt (Steifheit null erreicht).
Dm ist die Matrixschädigungsvariable (0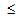 Dm
Dm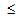 1) und wird berechnet durch
1) und wird berechnet durch
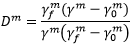
Dabei ist 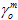 der Wert von
der Wert von 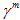 bei Schädigungsbeginn und
bei Schädigungsbeginn und 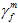 ist der Wert von
ist der Wert von 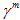 , wenn das Material vollständig zerfällt (Steifheit null erreicht).
, wenn das Material vollständig zerfällt (Steifheit null erreicht).
Es sollte erneut betont werden, dass die abgegebene Energie eines vollständig degradierten Materials direkt proportional zu 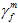 und
und 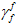 ist. Aus diesem Grund wird die Netzdichte verringert, indem
ist. Aus diesem Grund wird die Netzdichte verringert, indem 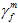 und
und 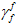 proportional zur Größe des Elements eingerichtet werden, wie angegeben durch
proportional zur Größe des Elements eingerichtet werden, wie angegeben durch
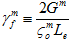
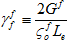
Dabei gilt: Gm und Gf entsprechen der abgegebenen Energiedichte der Verbundwerkstoffe, wenn die Matrix- und Faserkonstituenten ihre vollständig degradierten Bedingungen erreichen. 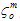 und
und 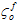 sind die effektiven Spannungen bei Schädigungsbeginn an Matrix und Fasern, und Le ist die effektive Länge des Elements.
sind die effektiven Spannungen bei Schädigungsbeginn an Matrix und Fasern, und Le ist die effektive Länge des Elements.
Diskrete Intervallunterteilung
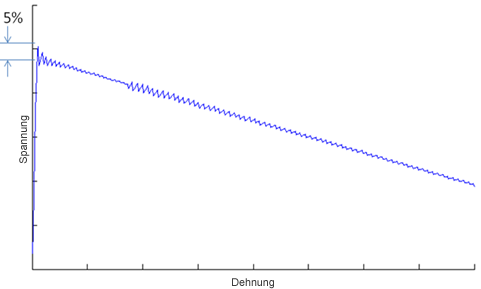
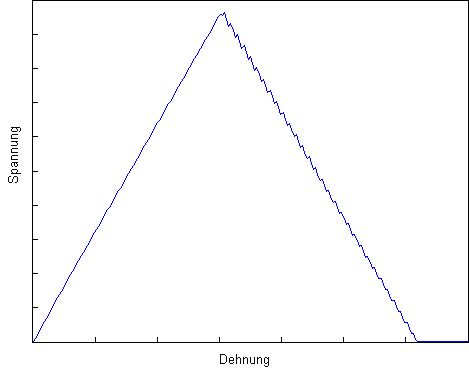
Die energiebasierte Schadensfunktion von Helius PFA verwendet mehrere einzelne Intervalle bei linearer Degradierung des Verbundwerkstoffs, wie unten dargestellt. Jedes Intervall verwendet ein Sekantenmodul zum Definieren der Reaktion des Verbundwerkstoffs in diesem Intervall. Bei Problemen, bei denen die Gesamtenergie etwa einem gleichschenkligen Dreieck entspricht, erfassen die Intervalle die Reaktion des Verbundwerkstoffs genau.
Bei Analysen, bei denen die Gesamtenergie ein sehr stark verzerrtes Dreieck darstellt, wie unten gezeigt, erfasst die Intervallteilung die lineare Abschwächung des Verbundwerkstoffs in frühen Dehnungsphasen nicht genau. Dies ist vollständig auf die Anzahl der Intervalle zurückzuführen, die für die schnelle und zuverlässige Behandlung des Problems verwendet werden. Besonders die Spannungssekantenintervalle bei Dehnungsgraden in Ausfallnähe behalten eine hohe Steifheit und können zu einer Fehlinterpretation des Spannungszustands des Verbundwerkstoffs führen. Wenn Ihnen Analysen vorliegen, die eine lineare Degradationskurve mit einer endgültigen effektiven Dehnung definieren, die über 100 Mal stärker als die anfängliche effektive Dehnung ist, wenden Sie sich an den Autodesk-Support.